【题目】穿越青海境内的兰新高速铁路正在加紧施工.某工程队承包了一段全长1957米的隧道工程,甲、乙两个班组分别从南北两端同时掘进,已知甲组比乙组每天多掘进0.5米,经过6天施工,甲、乙两组共掘进57米.
(1)求甲乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天比原来多掘进0.3米,乙组平均每天比原来多掘进0.2米.按此施工进度,能够比原来少用多少天完成任务?
参考答案:
【答案】(1)甲乙两个班组平均每天分别掘进5米、4.5米;(2)能比原来少用10天.
【解析】试题分析:(1)设甲、乙两个班组平均每天分别掘进x米、y米,根据题意列方程组,解方程组即可;(2)设按原来的施工进度和改进技术后的进度分别还需要a天、b天完成任务,分别计算出施工进度改进前和改进后完成任务还需的天数,再作差即可.
试题解析:
(1)设甲、乙两个班组平均每天分别掘进x米、y米,
由题意得![]() ,
,
解得![]() .
.
答:甲、乙两个班组平均每天分别掘进5米、4.5米;
(2)设按原来的施工进度和改进技术后的进度分别还需要a天、b天完成任务,则
a=(1957-57)÷(5+4.5)=200(天),
b=(1957-57)÷(5+4.5+0.2+0.3)=190(天),
则a-b=10(天).
答:能比原来少用10天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
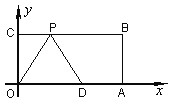
-
科目: 来源: 题型:
查看答案和解析>>【题目】春季流感爆发,某校为了解全体学生患流感情况,随机抽取部分班级对患流感人数的进行调查,发现被抽查各班级患流感人数只有1名、2名、3名、4名、5名、6名这六种情况,并制成如下两幅不完整的统计图:
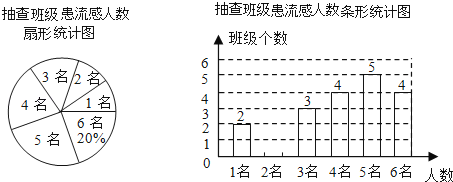
(1)抽查了 个班级,并将该条形统计图(图2)补充完整;
(2)扇形图(图1)中患流感人数为4名所在扇形的圆心角的度数为 ;
(3)若该校有45个班级,请估计该校此次患流感的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写下列空格,完成证明.
已知:如图,AD是△ABC的角平分线,点E在BC上,点F在CA的延长线上,EF∥AD,EF交AB于点G.
求证:∠3=∠F
证明:因为AD是△ABC的角平分线 ( 已知 )
所以∠1=∠2 ()
因为EF∥AD(已知)
所以∠3=∠()
∠F=∠()
所以∠3=∠F().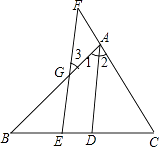
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC平分∠AOB,CD⊥OA于D,CE⊥OB于E,连接DE,猜想DE与OC的位置关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“若a>b,则|a|>|b|”是______命题.(填“真”或“假”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
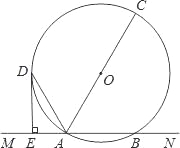
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
相关试题

