【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
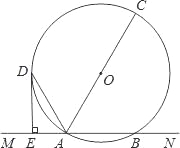
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
参考答案:
【答案】解:(1)证明:连接OD,
∵OA=OD,∴∠OAD=∠ODA。
∵∠OAD=∠DAE,∴∠ODA=∠DAE。∴DO∥MN。
∵DE⊥MN,∴∠ODE=∠DEM =90°,即OD⊥DE。
∵D在⊙O上,∴DE是⊙O的切线。
(2)连接CD,
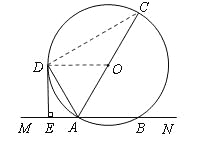
∵∠AED=90°,DE=6,AE=3,∴AD=![]() 。
。
∵AC是⊙O的直径,∴∠ADC=∠AED =90°。
∵∠CAD=∠DAE,∴△ACD∽△ADE。 ∴![]() ,即
,即![]() 。
。
解得:AC=15。
∴⊙O的半径是7.5cm。
【解析】试题分析:(1)连接OD,根据平行线的判断方法与性质可得∠ODE=∠DEM=90°,且D在⊙O上,故DE是⊙O的切线.
(2)由直角三角形的特殊性质,可得AD的长,又有△ACD∽△ADE.根据相似三角形的性质列出比例式,代入数据即可求得圆的半径.
试题解析:(1)证明:连接OD.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠OAD=∠DAE,
∴∠ODA=∠DAE.
∴DO∥MN.
∵DE⊥MN,
∴∠ODE=∠DEM=90°.
即OD⊥DE.
∵D在⊙O上,OD为⊙O的半径,
∴DE是⊙O的切线.
(2)解:∵∠AED=90°,DE=6,AE=3,
∴![]() .
.
连接CD.
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°.
∵∠CAD=∠DAE,
∴△ACD∽△ADE.
∴![]() .
.
∴![]() .
.
则AC=15(cm).
∴⊙O的半径是7.5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】穿越青海境内的兰新高速铁路正在加紧施工.某工程队承包了一段全长1957米的隧道工程,甲、乙两个班组分别从南北两端同时掘进,已知甲组比乙组每天多掘进0.5米,经过6天施工,甲、乙两组共掘进57米.
(1)求甲乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天比原来多掘进0.3米,乙组平均每天比原来多掘进0.2米.按此施工进度,能够比原来少用多少天完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC平分∠AOB,CD⊥OA于D,CE⊥OB于E,连接DE,猜想DE与OC的位置关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“若a>b,则|a|>|b|”是______命题.(填“真”或“假”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.

(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】1不是﹣1的( )
A.相反数B.绝对值C.平方数D.倒数
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A. 16人 B. 14人 C. 4人 D. 6人
相关试题

