【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.

(1)填空:A,B两地相距 千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?
参考答案:
【答案】(1)420;(2)y2=30x﹣60;
【解析】
试题分析:(1)由题意可知:B、C之间的距离为80千米,A、C之间的距离为360千米,所以A,B两地相距360+80=440千米;
(2)根据货车两小时到达C站,求得货车的速度,进一步求得到达A站的时间,进一步设y2与行驶时间x之间的函数关系式可以设x小时到达C站,列出关系式,代入点求得函数解析式即可;
(3)两函数的图象相交,说明两辆车相遇,求得y1的函数解析式,与(2)中的函数解析式联立方程,解决问题.
试题解析:(1)填空:A,B两地相距420千米;
(2)由图可知货车的速度为60÷2=30千米/小时,
货车到达A地一共需要2+360÷30=14小时,
设y2=kx+b,代入点(2,0)、(14,360)得
![]() ,
,
解得![]() ,
,
所以y2=30x﹣60;
(3)设y1=mx+n,代入点(6,0)、(0,360)得
![]() 解得
解得![]() ,
,
所以y1=﹣60x+360
由y1=y2得30x﹣60=﹣60x+360
解得x=![]()
答:客、货两车经过![]() 小时相遇.
小时相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次活动中,主办方共准备了3600盆甲种花和2900盆乙种花,计划用甲、乙两种花搭造出A、B两种园艺造型共50个,搭造要求的花盆数如下表所示:
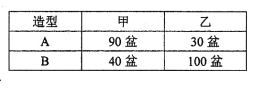
请问符合要求的搭造方案有几种?请写出具体的方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠BAC=
 ,∠ABC=
,∠ABC= ,∠BCA=
,∠BCA=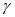 ,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。(1)若
 =78°,
=78°, =56°,
=56°,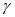 =46°,求∠EOH的大小;
=46°,求∠EOH的大小;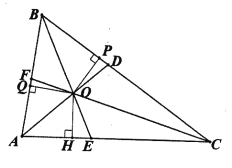
(2)用
 ,
, ,
,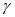 表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
表示∠EOH的表达式为∠EOH= ;(要求表达式最简)(3)若
 ≥
≥ ≥
≥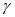 ,∠EOH+∠DOP+∠FOQ=
,∠EOH+∠DOP+∠FOQ= ,判断△ABC的形状并说明理由。
,判断△ABC的形状并说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内,已知点P(3,3),A(0,b)是y轴上一点,过P作PA的垂线交x轴于B(a,0),则称Q(a,b)为点P的一个关联点。
(1)写出点P的不同的两个关联点的坐标是 、 ;
(2)若点P的关联点Q(x,y)满足5x-3y=14,求出Q点坐标;

(3)已知C(-1,-1)。若点A、点B均在所在坐标轴的正半轴上运动,求△CAB的面积最大值,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】单位为了解3500名党员职工每月党费上交情况,从中随机抽取50名党员职工,根据每月每名党员职工的党费情况给制如图所示的条形统计图.
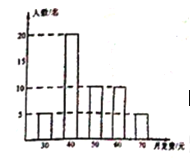
(1)求50名党职工每月觉费的平均数;
(2)直接写出这50名党员职工每月党费的众数与中位数;
(3)根据这50名党员职工每月党费的平均数,请你估计该单位3500名党员职工每月约上交党费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某市2016年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.

(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2016年10月份的水费为620元,求该企业2016年10月份的用水量;
(3)为鼓励企业节约用水,该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2016年收费标准收取水费外,超过80吨的部分每吨另加收
 元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量. -
科目: 来源: 题型:
查看答案和解析>>【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要900元;若购进甲种花卉40盆,乙种花卉30盆,需要960元.
(1)求购进甲、乙两种花卉每盆各需多少元?
(2)该花店购进甲,乙两种花卉共100盆,甲种花卉每盆售价20元,乙种花齐每盆售价16元,现该花店把100盆花卉全部售出,若获利超过480元,则至少购进甲种花卉多少盆?
相关试题

