【题目】在一次活动中,主办方共准备了3600盆甲种花和2900盆乙种花,计划用甲、乙两种花搭造出A、B两种园艺造型共50个,搭造要求的花盆数如下表所示:
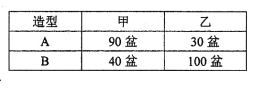
请问符合要求的搭造方案有几种?请写出具体的方案。
参考答案:
【答案】符合要求的搭造方案有3种;所有可行的方案有:
(1)A:30 个 B:20个
(2)A:31个 B:19个
(3)A:32个 B:18个
【解析】
可设A园艺造型x个,则B园艺造型(50-x)个,根据题意列出关于x的不等式组,由不等式组的解集确定符合要求的搭造方案即可.
解:设A园艺造型x个,B园艺造型(50-x)个,由题意可得:
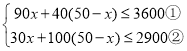
解不等式①得x≤32,
解不等式②得x≥30
∴原不等式组的解集是30≤x≤32
∴符合要求的搭造方案有3种
所以,所有可行的方案有:
A:30 个 B:20个
A:31个 B:19个
A:32个 B:18个
-
科目: 来源: 题型:
查看答案和解析>>【题目】图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时 间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
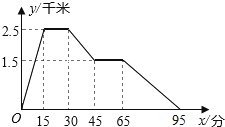
A. 体育场离张强家2.5千米
B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店1.千米
D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=
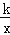 (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )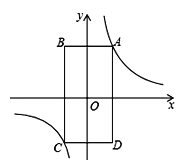
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=
 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠BAC=
 ,∠ABC=
,∠ABC= ,∠BCA=
,∠BCA=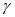 ,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。(1)若
 =78°,
=78°, =56°,
=56°,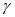 =46°,求∠EOH的大小;
=46°,求∠EOH的大小;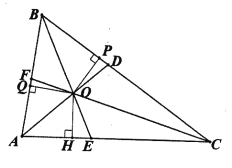
(2)用
 ,
, ,
,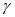 表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
表示∠EOH的表达式为∠EOH= ;(要求表达式最简)(3)若
 ≥
≥ ≥
≥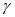 ,∠EOH+∠DOP+∠FOQ=
,∠EOH+∠DOP+∠FOQ= ,判断△ABC的形状并说明理由。
,判断△ABC的形状并说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内,已知点P(3,3),A(0,b)是y轴上一点,过P作PA的垂线交x轴于B(a,0),则称Q(a,b)为点P的一个关联点。
(1)写出点P的不同的两个关联点的坐标是 、 ;
(2)若点P的关联点Q(x,y)满足5x-3y=14,求出Q点坐标;

(3)已知C(-1,-1)。若点A、点B均在所在坐标轴的正半轴上运动,求△CAB的面积最大值,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.

(1)填空:A,B两地相距 千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?
相关试题

