【题目】已知在△ABC中,∠BAC=![]() ,∠ABC=
,∠ABC=![]() ,∠BCA=
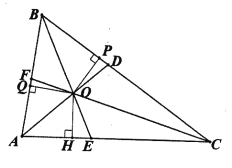
,∠BCA=![]() ,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
(1)若![]() =78°,
=78°,![]() =56°,
=56°,![]() =46°,求∠EOH的大小;
=46°,求∠EOH的大小;
(2)用![]() ,
,![]() ,
,![]() 表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
(3)若![]() ≥
≥![]() ≥
≥![]() ,∠EOH+∠DOP+∠FOQ=
,∠EOH+∠DOP+∠FOQ=![]() ,判断△ABC的形状并说明理由。
,判断△ABC的形状并说明理由。
参考答案:
【答案】(1)16°;(2)∠EOH=![]() +
+![]()
![]() -90°;(3)△ABC是直角三角形,理由见解析。
-90°;(3)△ABC是直角三角形,理由见解析。
【解析】
(1)由角平分线的性质求出∠EBA,再根据三角形内角和定理可知∠BEA,在Rt△OHE中可求得∠EOH的大小;
根据(1)中过程可表示;
由(2)同理可用![]() ,
,![]() ,
,![]() 表示∠DOP和∠FOQ,将∠EOH+∠DOP+∠FOQ=
表示∠DOP和∠FOQ,将∠EOH+∠DOP+∠FOQ=![]() 中的∠EOH,∠DOP和∠FOQ进行等量代换,可得出
中的∠EOH,∠DOP和∠FOQ进行等量代换,可得出![]() ,
,![]() ,
,![]() 间的关系,由此可判断△ABC的形状.
间的关系,由此可判断△ABC的形状.
解(1)∵BE平分∠ABC(已知) ∠ABC=![]() (已知)
(已知)
∴∠EBA=![]() ∠ABC=
∠ABC=![]()
![]() (角平分线性质)
(角平分线性质)
∵∠BAC=![]() (已知)
(已知)
∴∠BEA=180°-∠BAC-∠EBA=180°-![]() -
-![]()
![]() (三角形内角和180°)
(三角形内角和180°)
∵OH⊥AC(已知)
∴∠OHE=90°(垂直的定义)
∴在Rt△OHE中,∠EOH=90°-∠OEH=90-∠BEA=90-(180°-![]() -
-![]()
![]() )=16°
)=16°
(2) 由(1)知 ∠EOH=![]() +
+![]()
![]() -90°
-90°
(3) 由(2)同理得∠DOP=![]() +
+![]()
![]() - 90° ,∠FOQ=
- 90° ,∠FOQ=![]() +
+![]()
![]() -90°
-90°
∠EOH+∠DOP+∠FOQ=![]() +
+![]()
![]() -90°+
-90°+![]() +
+![]()
![]() - 90°+
- 90°+![]() +
+![]()
![]() -90°=
-90°=![]()
解得![]() α+
α+![]() (β+γ)=270°
(β+γ)=270°
∵β+γ=180°-α(三角形内角和180°)
![]()
解得α=90°
∴ △ABC是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=
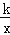 (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )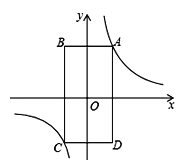
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=
 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次活动中,主办方共准备了3600盆甲种花和2900盆乙种花,计划用甲、乙两种花搭造出A、B两种园艺造型共50个,搭造要求的花盆数如下表所示:
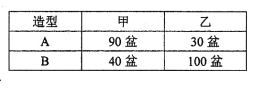
请问符合要求的搭造方案有几种?请写出具体的方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内,已知点P(3,3),A(0,b)是y轴上一点,过P作PA的垂线交x轴于B(a,0),则称Q(a,b)为点P的一个关联点。
(1)写出点P的不同的两个关联点的坐标是 、 ;
(2)若点P的关联点Q(x,y)满足5x-3y=14,求出Q点坐标;

(3)已知C(-1,-1)。若点A、点B均在所在坐标轴的正半轴上运动,求△CAB的面积最大值,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.

(1)填空:A,B两地相距 千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】单位为了解3500名党员职工每月党费上交情况,从中随机抽取50名党员职工,根据每月每名党员职工的党费情况给制如图所示的条形统计图.
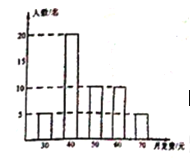
(1)求50名党职工每月觉费的平均数;
(2)直接写出这50名党员职工每月党费的众数与中位数;
(3)根据这50名党员职工每月党费的平均数,请你估计该单位3500名党员职工每月约上交党费多少元?
相关试题

