【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.

参考答案:
【答案】(1)证明见解析;(2)①5;②证明见解析.
【解析】
(1)延长CB到G,使GB=DF,连接AG,求证△ABG≌△ADF,得∠3=∠2,AG=AF,进而求证△AGE≌△AFE,可得GB+BE=EF,所以DF+BE=EF.
(2)①如图2,把△ABM绕点A逆时针旋转90°得到△ADM′,连接NM′.就可以得出△ABM≌△ADM′,就有∠BAM=∠DAM′,就可以得出△AMN≌△AM′N就可以得出MN=M′N,由勾股定理就可以得出结论MN2=DN2+BM2;
②设正方形ABCD的边长为a,求出MN,EC即可判断;
(1)证明:证明:延长CB到G,使GB=DF,连接AG(如图1),
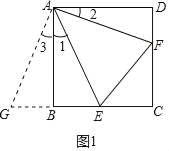
∵AB=AD,∠ABG=∠D=90°,GB=DF,
∴△ABG≌△ADF(SAS),
∴∠3=∠2,AG=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠1+∠2=45°,
∴∠GAE=∠1+∠3=45°=∠EAF,
∵AE=AE,∠GAE=∠EAF,AG=AF,
∴△AGE≌△AFE(SAS),
∴GB+BE=EF,
∴DF+BE=EF;
(2)①解:如图2,在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠ABM=∠ADN=45°.
把△ABM绕点A逆时针旋转90°得到△ADM'.连结NM'.
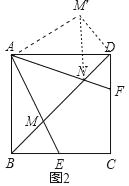
∴△ABM≌△ADM′(旋转不变性),
∴DM'=BM,AM'=AM,∠ADM'=∠ABM=45°,∠DAM'=∠BAM.
∴∠ADB+∠ADM′=45°+45°=90°,
即∠NDM′=90°.
∵∠EAF=45°,
∴∠BAM+∠DAN=45°,
∴∠DAM′+∠DAF=45°,
即∠M′AN=45°,
∴∠M'AN=∠MAN.
在△AMN和△AM′N中
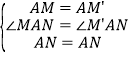 ,
,
∴△AMN≌△AM′N(SAS),
∴M'N=MN.
∵∠NDM′=90°,
∴M'N2=DN2+DM'2,
∴MN2=DN2+BM2;
设MN=x,则DN=12﹣3﹣x=9﹣x,
∴x2=33+(9﹣x)2,
∴x=5,
∴NM=5;
②证明:如图3中,设正方形ABCD的边长为a.
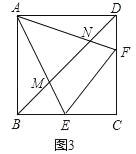
∵EF∥BD,
∴∠CEF=∠CBD=45°,∠CFE=∠CDB=45°,
∴∠CEF=∠CFE=45°,
∴CE=CF,
∴BE=DF,
∵AB=AD,∠ABE=∠ADF,BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,
∵∠EAF=45°,
∴∠BAE=∠DAF=22.5°,
∴∠AEB=∠BME=67.5°,
∴BM=BE,同理可证:DN=DF,
∴BM=DN=BE=DF,设BM=x,则MN=![]() x,
x,
∴2x+![]() x=
x=![]() a,
a,
∴x=(![]() ﹣1)a,
﹣1)a,
∴MN=(2﹣![]() )a,EC=BC﹣BE=(2﹣
)a,EC=BC﹣BE=(2﹣![]() )a,
)a,
∴MN=EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机动车辆出发前油箱中有油
 升,行驶若干小时后,在途中加油站加油若干.油箱中余油量
升,行驶若干小时后,在途中加油站加油若干.油箱中余油量 (升)与行驶时间
(升)与行驶时间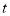 (时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(1)机动车辆行驶了 小时后加油,中途加油________升.
(2)加油后油箱中的油最多可行驶多少小时?
(3)若加油站距目的地还有
 公里,机动车每小时走
公里,机动车每小时走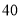 公里,油箱中的油能否使车到达目的地?
公里,油箱中的油能否使车到达目的地? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系上,已知点A(8,4),AB⊥y轴于B,AC⊥x轴于C,直线y=x交AB于D.
(1)直接写出B、C、D三点坐标;
(2)若E为OD延长线上一动点,记点E横坐标为a,△BCE的面积为S,求S与a的关系式;
(3)当S=20时,过点E作EF⊥AB于F,G、H分别为AC、CB上动点,求FG+GH的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解决下面的问题
(一)如图,大正方形是由两个小正方形和两个长方形拼成的.

(1)请你用两个不同形式的代数式表示这个大正方形的面积;
代数式
 :
: 代数式
 :
: (2)由
 可得到关于
可得到关于 的等式:
的等式: (二)从边长为
 的大正方形纸板中挖去一个边长为
的大正方形纸板中挖去一个边长为 的小正方形纸板后,将其裁成四个相同的等腰梯形(图甲),然后拼成一个平行四边形(图乙). 那么通过计算两个图形阴影部分的面积,可以验证成立的乘法公式是 (用字母表示)
的小正方形纸板后,将其裁成四个相同的等腰梯形(图甲),然后拼成一个平行四边形(图乙). 那么通过计算两个图形阴影部分的面积,可以验证成立的乘法公式是 (用字母表示) 
(3)计算
 (直接写结果)
(直接写结果)
用上面的卡片,(数量自定)画出一个图形,来验证上面的整式运算(要求图中有长度和面积的标记)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.

(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=
 AB.
AB.灵活应用:如图2,△ABC中,∠BAC=90°,AB=6,AC=8,点D是BC的中点,连接AD,将△ACD沿AD翻折得到△AED,连接BE,CE.
(1)填空:AD= ;
(2)求证:∠BEC=90°;
(3)求BE.

相关试题

