【题目】由![]() 个完全相同的小正方体搭成的物体如图所示.
个完全相同的小正方体搭成的物体如图所示.
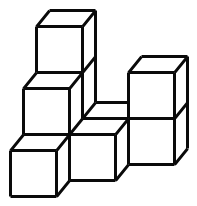
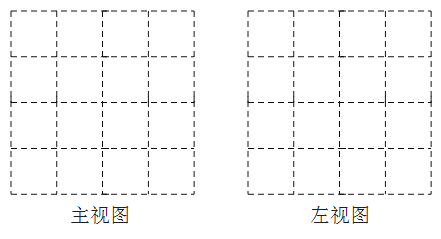
(1)请在下面的方格图中画出该物体的主视图和左视图;
(2)如果再添加若干个相同的小正方体之后,所得到的新物体的主视图和左视图跟原来的相间,那么这样的小正方体最多还可以添加 个.
参考答案:
【答案】(1)详见解析; (2)![]() .
.
【解析】
(1)根据几何体的小正方体的个数,即可画出几何体的主视图和左视图;
(2)底层第二列第一行加1个,第三列第一、二分别加1个;第二层第三列第二行加1个,共4共4个.
解:(1)如图所示,
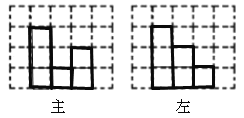
(2)如果在这个几何体上再添加一些相同的小正方体,并保持其主视图和左视图不变,那么最多可以再添加 4个小正方体(如图中A、B、C、D):
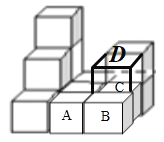
∴最多可以再添加4个小正方体.
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
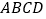 中,
中, 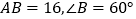 ,
,  是
是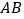 上一点,
上一点, ,
, 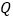 是
是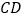 边上一动点,将四边形
边上一动点,将四边形 沿宜线
沿宜线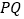 折叠,
折叠,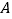 的对应点
的对应点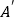 .当
.当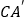 的长度最小时,则
的长度最小时,则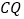 的长为( )
的长为( )
A.
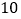 B.
B.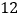 C.
C.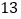 D.
D.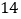
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
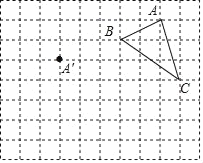
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代对于利用方程解决实际问题早有研究,《九章算术》中提到这么一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺:若将绳四折测之,绳多一尺.绳长、井深各几何?
这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺:如果将绳子折成四等份,那么每等份井外余绳一尺.问绳长和井深各多少尺?若设井深为x尺,则求解井深的方程正确的是( )
A.3(x+4)=4(x+1)B.3x+4=4x+1
C.
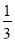 x+4=
x+4=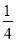 x+1D.
x+1D.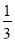 x﹣4=
x﹣4=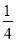 x﹣1
x﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和父母打算去某火锅店吃火锅,该店在网上出售“
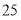 元抵
元抵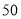 元的全场通用代金券”(即面值
元的全场通用代金券”(即面值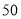 元的代金券实付
元的代金券实付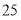 元就能获得),店家规定代金券等同现金使用,一次消费最多可用
元就能获得),店家规定代金券等同现金使用,一次消费最多可用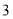 张代金券,而且使用代金券的金额不能超过应付总金额.
张代金券,而且使用代金券的金额不能超过应付总金额.(1)如果小明一家应付总金额为
 元,那么用代金券方式买单,他们最多可以优惠多少元:
元,那么用代金券方式买单,他们最多可以优惠多少元:(2)小明一家来到火锅店后,发现店家现场还有一个优惠方式: 除锅底不打折外,其余菜品全部
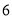 折.小明一家点了一份
折.小明一家点了一份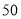 元的锅底和其他菜品,用餐完毕后,聪明的小明对比两种优惠,选择了现场优惠方式买单,这样比用代金券方式买单还能少付
元的锅底和其他菜品,用餐完毕后,聪明的小明对比两种优惠,选择了现场优惠方式买单,这样比用代金券方式买单还能少付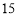 元.问小明一家实际付了多少元?
元.问小明一家实际付了多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
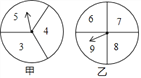
(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】童星玩具厂工人的工作时间为:每月22天,每天8小时.工资待遇为:按件计酬,多劳多得,每月另加福利工资500元,按月结算.该厂生产A、B两种产品,工人每生产一件A种产品可得报酬1.50元,每生产一件B种产品可得报酬2.80元.该厂工人可以选择A、B两种产品中的一种或两种进行生产.工人小李生产1件A产品和1件B产品需35分钟;生产3件A产品和2件B产品需85分钟.
(1)小李生产1件A产品需要 分钟,生产1件B产品需要 分钟.
(2)求小李每月的工资收入范围.
相关试题

