【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
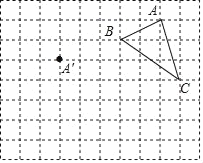
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
参考答案:
【答案】(1)![]() ;(2)见解析;(3)平行且相等.
;(2)见解析;(3)平行且相等.
【解析】
(1)利用割补法求解可得;
(2)由点A及其对应点A′得出平移方式为:先向左移5格,再向下移2格,据此作出点B和点C的对应点,再顺次连接即可得;
(3)根据平移变换的性质可得答案.
解:(1)△ABC的面积是3×3﹣![]() ×1×2﹣
×1×2﹣![]() ×2×3﹣
×2×3﹣![]() ×1×3=
×1×3=![]() ,
,
故答案为:![]() ;
;
(2)如图所示,△A'B'C'即为所求,

(3)若连接AA'、CC′,这两条线段的关系是平行且相等,
故答案为:平行且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点 P 在平面直角坐标系中按图中箭头所示方向运动,第 1 次从原点运动到点(1,1),第 2 次接着运动到点(2,0),第 3 次接着运动到点(3,2),……,按这样的运动规律,经过第2025 次运动后,动点 P 的坐标是( )
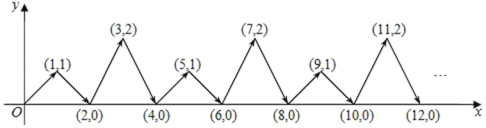
A.(2025,1)B.(2025,0)C.(2026,2)D.(2026,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数 y=kx+b,当 1≤x≤4 时,3≤y≤6,则一次函数的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
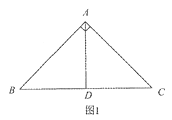
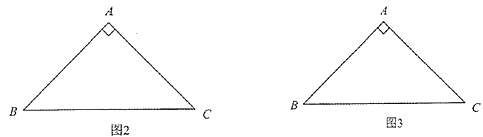
已知在Rt△ABC中,∠BAC=90°,AB=AC=2
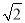 .
.(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
-
科目: 来源: 题型:
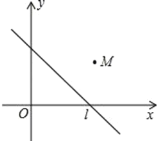
查看答案和解析>>【题目】如图,已知点 M 的坐标为(4,3),点 M 关于直线 l:y=﹣x+b 的对称点落在坐标轴上,则 b的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一节数学课上,老师出示了这样一个问题让学生探究:
已知:如图在△ABC中,点D 是BA边延长线上一动点,点F 在BC上,且
 ,连接DF交AC于点E .
,连接DF交AC于点E . (1)如图1,当点E恰为DF的中点时,请求出
 的值;
的值;(2)如图2,当
 时,请求出
时,请求出 的值(用含a的代数式表示).
的值(用含a的代数式表示).思考片刻后,同学们纷纷表达自己的想法:
甲:过点F作FG∥AB交AC于点G,构造相似三角形解决问题;
乙:过点F作FG∥AC交AB于点G,构造相似三角形解决问题;
丙:过点D作DG∥BC交CA延长线于点G,构造相似三角形解决问题;
老师说:“这三位同学的想法都可以” .
请参考上面某一种想法,完成第(1)问的求解过程,并直接写出第(2)问
 的值.
的值. 

图1 图2
相关试题

