【题目】“树德之声”结束后,王老师和李老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如图频数直方图和扇形统计图:
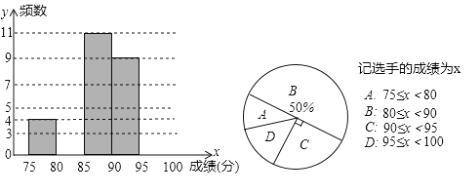
(1)求本次比赛参赛选手总人数,并补全频数直方图;
(2)求扇形统计图中扇形D的圆心角度数;
(3)成绩在D区域的选手中,男生比女生多一人,从中随机抽取两人,求恰好选中一名男生和一名女生的概率.
参考答案:
【答案】(1)本次比赛参赛选手总人数36人,补图见解析;(2)50°;(3)![]() .
.
【解析】
(1)先求出C区域的人数和所占的百分比,然后用C区域的人数除以其所占的百分比,即可求得总人数,再用总人数乘以每个区域所占的百分比求出每个区域的人数,最后完成直方图即可;
(2)用360°乘以D区域的人数所占的百分比即可;
(3)先求出D区域男生、女生的人数,再画树状图求出等可能的结果数和所求的结果数,最后根据概率公式求解即可.
解:(1)本次比赛参赛选手总人数是9÷![]() =36(人),
=36(人),
80≤x<90的人数有:36×50%=18(人),
则80≤x<85的人数有18﹣11=7(人),
95≤x<100的人数有:36﹣4﹣18﹣9=5(人),补图如下:
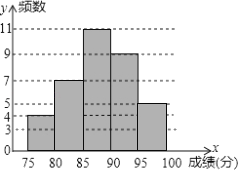
(2)求扇形统计图中扇形D的圆心角度数是360°×![]() =50°;
=50°;
(3)∵D区域的选手共有5人,其中男生比女生多一人,
∴男生有3人,女生有2人,
画图如下:

共有20种等情况数,其中选中一名男生和一名女生的有12种,
则恰好选中一名男生和一名女生的概率是![]() .
.
-
科目: 来源: 题型:
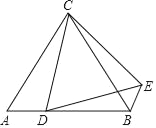
查看答案和解析>>【题目】如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D,若BC=6,sin∠BAC=
 ,则AC=_____,CD=_____.
,则AC=_____,CD=_____.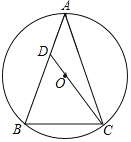
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=2
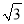 ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.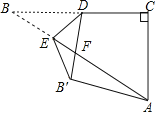
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小花在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小花身高1.5米,当她从点A跑动9
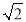 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=
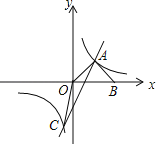
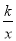 交于A、C两点,AB⊥OA交x轴于点B,且AB=OA.
交于A、C两点,AB⊥OA交x轴于点B,且AB=OA.(1)求双曲线的解析式;
(2)连接OC,求△AOC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接BD、DE.
(1)求DE是⊙O的切线;
(2)设△CDE的面积为S1,四边形ABED的面积为S2,若S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,连接AE,若⊙O的半径为2,求AE的长.

相关试题

