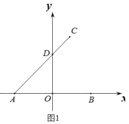
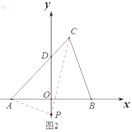
【题目】如图 1,在平面直角坐标系中,已知点A(a,0),B(b,0),C(2,7),连接 AC,交y轴于 D,且![]() ,
,![]() .
.
(1)求点D的坐标.
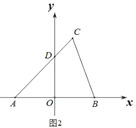
(2)如图 2,y轴上是否存在一点P,使得△ACP的面积与△ABC的面积相等?若存在,求点P的坐标,若不存在,说明理由.
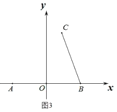
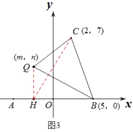
(3)如图 3,若 Q(m,n)是 x轴上方一点,且![]() 的面积为20,试说明:7m+3n是否为定值,若为定值,请求出其值,若不是,请说明理由.
的面积为20,试说明:7m+3n是否为定值,若为定值,请求出其值,若不是,请说明理由.
参考答案:
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)
;(3)![]() 的值为
的值为![]() 或75
或75
【解析】
(1)根据立方根与算术平方根的定义求出a,b,连接![]() ,设
,设![]() ,根据
,根据![]() 求出x的值即可;
求出x的值即可;
(2)先求出△ABC的面积,设点![]() 的坐标为
的坐标为![]() ,根据
,根据![]() 列式求解;
列式求解;
(3)分两种情况考虑,当点![]() 在直线
在直线![]() 的左侧时与当点
的左侧时与当点![]() 在直线
在直线![]() 的右侧时,过
的右侧时,过![]() 点作
点作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() ,根据
,根据![]() 进行求解.
进行求解.
解:(1)∵![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
如图1,连接![]() ,设
,设![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)如图2,由![]() ,
,![]() ,
,![]() 三点的坐标可求
三点的坐标可求![]() ,
,
∵点![]() 在
在![]() 轴上,
轴上,
∴设点![]() 的坐标为
的坐标为![]() ,
,
由![]() ,且点
,且点![]() 的坐标为
的坐标为![]() ,
,
![]()
解得:![]() 或15,
或15,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
(3)∵点![]() 在
在![]() 轴上方,
轴上方,
如图3,当点![]() 在直线
在直线![]() 的左侧时,
的左侧时,
过![]() 点作
点作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() ,
,
由![]() ,且
,且![]()
![]()
![]() ;
;
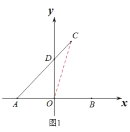
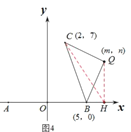
如图4,当点![]() 在直线
在直线![]() 的右侧时,
的右侧时,
过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() ,
,
由![]() ,且
,且![]() ,
,
![]() ,
,
![]() ,
,
综上所述,![]() 的值为
的值为![]() 或75.
或75.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点P(3,4)绕原点逆时针旋转90°,得到的点P的对应点的坐标为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:两直线l1,l2满足l1∥l2 ,点C,点D在直线l1上,点A,点B在直线l2上,点P是平面内一动点,连接CP,BP,
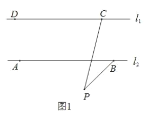
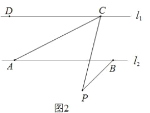
(1)如图 1,若点P在 l1,l2外部,则∠DCP、∠CPB、∠ABP之间满足什么数量关系?请你证明的这个结论;
(2)如图 2,若点P在l1,l2外部,连接AC,则∠CAB、∠ACP、∠CPB、∠ABP之间满足什么数量关系?请你证明这个结论;(不能用三角形内角和为 180°)
(3)若点P在 l1,l2内部,且在AC的右侧,则∠ACP﹑∠ABP﹑∠CAB﹑∠CPB之间满足什么数量关系?(不需证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD=
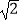 ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 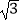 ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )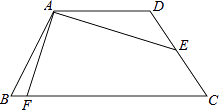
A.1
B.3﹣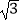
C.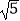 ﹣1
﹣1
D.4﹣2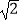
-
科目: 来源: 题型:
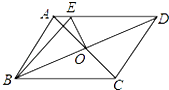
查看答案和解析>>【题目】如图,在周长为20cm的ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正三角形ABC与正三角形CDE,若∠DBE=66°,则∠ADB度数为__________.
相关试题

