【题目】如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q. 
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ![]() ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.
参考答案:
【答案】
(1)解:CD与⊙O相切.理由如下:
连结OC,如图,

∵OC=OB,
∴∠2=∠B,
∵DQ=DC,
∴∠1=∠Q,
∵QP⊥PB,
∴∠BPQ=90°,
∴∠Q+∠B=90°,
∴∠1+∠2=90°,
∴∠DCO=180°﹣∠1﹣∠2=90°,
∴OC⊥CD,
而OC为⊙O的半径,
∴CD为⊙O的切线;
(2)解:连接AC,如图,

∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,cosB= ![]() =
= ![]() =
= ![]() ,
,
而BP=6,AP=1,
∴BC= ![]() ,
,
在Rt△BPQ中,cosB= ![]() =
= ![]() ,
,
∴BQ= ![]() =10,
=10,
∴QC=BQ﹣BC=10﹣ ![]() =
= ![]() .
.
【解析】(1)连结OC,由OC=OB得∠2=∠B,DQ=DC得∠1=∠Q,根据QP⊥PB得到∠Q+∠B=90°,则∠1+∠2=90°,再利用平角的定义得到∠DCO=90°,然后根据切线的判定定理得到CD为⊙O的切线;(2)连结AC,由AB为⊙O的直径得∠ACB=90°,根据余弦的定义得cosB= ![]() =
= ![]() =
= ![]() ,可计算出BC=
,可计算出BC= ![]() ,在Rt△BPQ中,利用余弦的定义得cosB=
,在Rt△BPQ中,利用余弦的定义得cosB= ![]() =
= ![]() ,可计算出BQ=10,然后利用QC=BQ﹣BC进行计算即可.
,可计算出BQ=10,然后利用QC=BQ﹣BC进行计算即可.
【考点精析】关于本题考查的切线的判定定理和解直角三角形,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0; ④
 的最小值为3.其中正确的是( )
的最小值为3.其中正确的是( )
A.①②③
B.②③④
C.①③④
D.①②③④ -
科目: 来源: 题型:
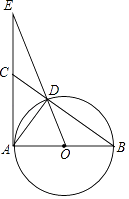
查看答案和解析>>【题目】已知,如图,Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于D,OD交AC的延长线于E,OA=1,AE=3.则下列结论正确的有 . ①∠B=∠CAD;②点C是AE的中点;③
 =
= 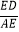 ;④tan B=
;④tan B= 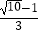 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.
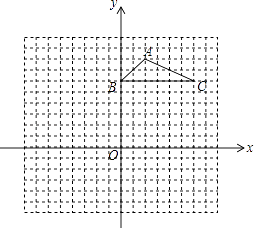
①将△ABC向左平移7个单位后再向下平移3个单位,请画出两次平移后的△A1B1C1 , 若M为△ABC内的一点,其坐标为(a,b),直接写出两次平移后点M的对应点M1的坐标;
②以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1:2.请在网格内画出在第三象限内的△A2B2C2 , 并写出点A2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).

-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强公路的节水意识,合理利用水资源,某市对居民用水实行阶梯水价,居民家庭每月用水量划分为两个阶梯,一、二阶梯用水的单价之比等于1:2,如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系,其中射线AB表示第二级阶梯时y与x之间的函数关系.

(1)写出点B的实际意义;
(2)求射线AB所在直线的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x﹣2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c,若y1﹣y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当﹣3≤x≤3时,y2的最大值.
相关试题

