搜索
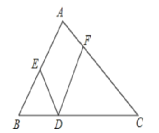
【题目】如图所示，在△ABC中，点D. E. F分别在BC、AB、AC上，且BD=BE，CD=CF，∠EDF=50°.则∠A的度数为___________．
参考答案：
【答案】80°
【解析】
由∠EDF=50°可得∠BDE+∠CDF=130°，根据三角形内角和定理可求出∠B+∠C，就可求出∠A．
∵BD=BE，CD=CF，
∴∠BDE=∠BED，∠CDF=∠CFD.
∵∠BDE+∠EDF+∠CDF=180°，∠EDF=50°，
∴∠BDE+∠CDF=130°.
∵∠B+∠BDE+∠BED=180°，∠C+∠CDF+∠CFD=180°，
∴∠B+∠BDE+∠BED+∠C+∠CDF+∠CFD=360°.
∴∠B+∠C+2∠BDE+2∠CDF=360°.
∴∠B+∠C+260°=360°.
∴∠B+∠C=100°.
∵∠A+∠B+∠C=180°，
∴∠A=80°.
故答案为:80°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着社会的发展，通过微信朋友圈发布自己每天行走的步数已经成为一种时尚．“健身达人”小陈为了了解他的好友的运动情况．随机抽取了部分好友进行调查，把他们6月1日那天行走的情况分为四个类别：A（0～5000步）（说明：“0～5000”表示大于等于0，小于等于5000，下同），B（5001～10000步），C（10001～15000步），D（15000步以上），统计结果如图所示：
请依据统计结果回答下列问题：
（1）本次调查中，一共调查了 位好友．
（2）已知A类好友人数是D类好友人数的5倍．
①请补全条形图；
②扇形图中，“A”对应扇形的圆心角为 度．
③若小陈微信朋友圈共有好友150人，请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步？
-
科目： 来源： 题型：
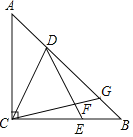
查看答案和解析>>【题目】如图，等腰Rt△ABC中，∠ACB=90°，AC=BC，点D、E分别在边AB、CB上，CD=DE，∠CDB=∠DEC，过点C作CF⊥DE于点F，交AB于点G，
（1）求证：△ACD≌△BDE；
（2）求证：△CDG为等腰三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某年5月，我国南方某省A、B两市遭受严重洪涝灾害，1.5万人被迫转移，邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后，决定调运物资支援灾区．已知C市有救灾物资240吨，D市有救灾物资260吨，现将这些救灾物资全部调往A、B两市．已知从C市运往A、B两市的费用分别为每吨20元和25元，从D市运往往A、B两市的费用别为每吨15元和30元，设从D市运往B市的救灾物资为x吨．
（1）请填写下表
A（吨）
B（吨）
合计（吨）
C
240
D
x
260
总计（吨）
200
300
500
（2）设C、D两市的总运费为w元，求w与x之间的函数关系式，并写出自变量x的取值范围；
（3）经过抢修，从D市到B市的路况得到了改善，缩短了运输时间，运费每吨减少m元（m＞0），其余路线运费不变．若C、D两市的总运费的最小值不小于10320元，求m的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，E、F分别为线段AB、AC上的点（不与A、B、C重合）．
（1）如图1，若EF∥BC，求证：
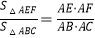
（2）如图2，若EF不与BC平行，（1）中的结论是否仍然成立？请说明理由；
（3）如图3，若EF上一点G恰为△ABC的重心，
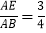，求
的值．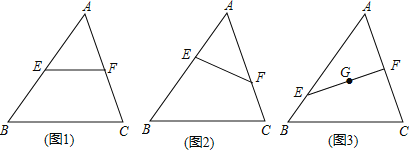
-
科目： 来源： 题型：
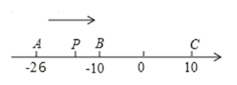
查看答案和解析>>【题目】已知数轴上有 A、B、C 三点，分别表示有理数－26，－10，10，动点 P 从 A 出发，以每秒 1 个 单位的速度向终点 C 移动，设点 P 移动时间为 t 秒．
（1）用含 t 的代数式表示 P 到点 A 和点C 的距离：PA= ，PC=
（2）当点 P 运动到 B 点时，点 Q 从 A 点出发，以每秒 3 个单位的速 度向 C 点运动，Q 点到达 C 点后，再立即以同样的速度返回，当点 P 运动到点 C 时，P、Q 两点运动停止，
①当 P、Q 两点运动停止时，求点 P 和点 Q 的距离；
②求当 t 为何值时 P、Q 两点恰好在途中相遇．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=a（x﹣1）2过点（3，1），D为抛物线的顶点．
（1）求抛物线的解析式；
（2）若点B、C均在抛物线上，其中点B（0，
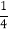），且∠BDC=90°，求点C的坐标；（3）如图，直线y=kx+4﹣k与抛物线交于P、Q两点．
①求证：∠PDQ=90°；
②求△PDQ面积的最小值．
相关试题
