【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:

请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
参考答案:
【答案】(1)30;(2)①补图见解析;②120;③70人.
【解析】(1)由B类别人数及其所占百分比可得总人数;
(2)①设D类人数为a,则A类人数为5a,根据总人数列方程求得a的值,从而补全图形;
②用360°乘以A类别人数所占比例可得;
③总人数乘以样本中C、D类别人数和所占比例.
(1)本次调查的好友人数为6÷20%=30人,
故答案为:30;
(2)①设D类人数为a,则A类人数为5a,
根据题意,得:a+6+12+5a=30,
解得:a=2,
即A类人数为10、D类人数为2,
补全图形如下:

②扇形图中,“A”对应扇形的圆心角为360°×![]() =120°,
=120°,
故答案为:120;
③估计大约6月1日这天行走的步数超过10000步的好友人数为150×![]() =70人.
=70人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果种植场今年收获的“妃子笑”和“无核Ⅰ号”两种荔枝共3200 千克,全部售出后卖了30400 元.已知“妃子笑”荔枝每千克售价8 元,“无核Ⅰ号”荔枝每千克售价12 元,问该种植场今年这两种荔枝各收获多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】人和人之间讲友情,有趣的是,数与数之间也有相类似的关系. 若两个不同的自然数的所有真因数(即除了自身以外的正约数)之和相等,我们称这两个数为“亲和数”. 例如:18的约数有1、2、3、6、9、18,它的真因数之和1+2+3+6+9=21;51的约数有1、3、17、51,它的真因数之和1+3+17=21,所以18和51为“亲和数”. 数还可以与动物形象地联系起来,我们称一个两头(首位与末位)都是
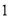 的数为“两头蛇数”.
的数为“两头蛇数”.(1)6的“亲和数”为 ;将一个四位的“两头蛇数”去掉两头,得到一个两位数,它恰好是这个“两头蛇数”的约数,求满足条件的“两头蛇数”.
(2)已知两个“亲和数”的真因数之和都等于15,且这两个“亲和数”中较大的数能将一个正中间数位(百位)上的数为4的五位“两头蛇数”整除,若这个五位“两头蛇数”的千位上的数字小于十位上的数字,求满足条件的“两头蛇数”.
-
科目: 来源: 题型:
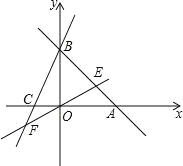
查看答案和解析>>【题目】直线AB:y=﹣x+b分别与x,y轴交于A(6,0)、B 两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
(1)求点B的坐标.
(2)求直线BC的解析式.
(3)直线 EF 的解析式为y=x,直线EF交AB于点E,交BC于点 F,求证:S△EBO=S△FBO.
-
科目: 来源: 题型:
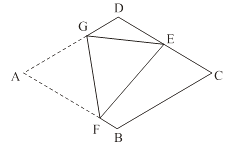
查看答案和解析>>【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为 .
-
科目: 来源: 题型:
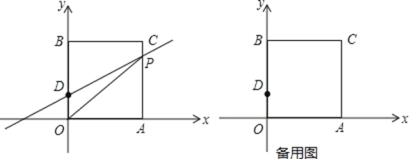
查看答案和解析>>【题目】如图在平面直角坐标系中,O 是坐标原点,长方形 OACB 的顶点 A,B 分别在 x,y 轴上,已知 OA=3, 点 D 为 y 轴上一点,其坐标为(0,1),CD=5,点 P 从点 A 出发以每秒 1 个单位的速度沿线段 A﹣C﹣B 的方向运动,当点 P 与点 B 重合时停止运动,运动时间为 t 秒
(1)求 B,C 两点坐标;
(2)①求△OPD 的面积 S 关于 t 的函数关系式;
②当点 D 关于 OP 的对称点 E 落在 x 轴上时,求点 E 的坐标;
(3)在(2)②情况下,直线 OP 上求一点 F,使 FE+FA 最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,从下列条件中补充一个条件后,仍不能判定
,从下列条件中补充一个条件后,仍不能判定 的是( )
的是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

