【题目】已知抛物线y=a(x﹣1)2过点(3,1),D为抛物线的顶点.
(1)求抛物线的解析式;
(2)若点B、C均在抛物线上,其中点B(0,![]() ),且∠BDC=90°,求点C的坐标;
),且∠BDC=90°,求点C的坐标;
(3)如图,直线y=kx+4﹣k与抛物线交于P、Q两点.
①求证:∠PDQ=90°;
②求△PDQ面积的最小值.

参考答案:
【答案】(1)y=![]() (x﹣1)2;(2)点C的坐标为(17,64).(3)①证明见解析;②16.
(x﹣1)2;(2)点C的坐标为(17,64).(3)①证明见解析;②16.
【解析】(1)将点(3,1)代入解析式求得a的值即可;
(2)设点C的坐标为(x0,y0),其中y0=![]() (x0﹣1)2,作CF⊥x轴,证△BDO∽△DCF得
(x0﹣1)2,作CF⊥x轴,证△BDO∽△DCF得![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() 据此求得x0的值即可得;
据此求得x0的值即可得;
(3)①设点P的坐标为(x1,y1),点Q为(x2,y2),联立直线和抛物线解析式,化为关于x的方程可得![]() ,据此知(x1﹣1)(x2﹣1)=﹣16,由PM=y1=
,据此知(x1﹣1)(x2﹣1)=﹣16,由PM=y1=![]() (x1﹣1)2、QN=y2=
(x1﹣1)2、QN=y2=![]() (x2﹣1)2、DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1知PMQN=DMDN=16,即
(x2﹣1)2、DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1知PMQN=DMDN=16,即![]() =
=![]() ,从而得△PMD∽△DNQ,据此进一步求解可得;
,从而得△PMD∽△DNQ,据此进一步求解可得;
②过点D作x轴的垂线交直线PQ于点G,则DG=4,根据S△PDQ=![]() DGMN列出关于k的等式求解可得.
DGMN列出关于k的等式求解可得.
(1)将点(3,1)代入解析式,得:4a=1,
解得:a=![]() ,
,
所以抛物线解析式为y=![]() (x﹣1)2;
(x﹣1)2;
(2)由(1)知点D坐标为(1,0),
设点C的坐标为(x0,y0),(x0>1、y0>0),
则y0=![]() (x0﹣1)2,
(x0﹣1)2,
如图1,过点C作CF⊥x轴,
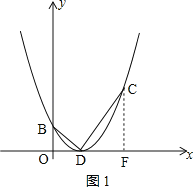
∴∠BOD=∠DFC=90°、∠DCF+∠CDF=90°,
∵∠BDC=90°,
∴∠BDO+∠CDF=90°,
∴∠BDO=∠DCF,
∴△BDO∽△DCF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
解得:x0=17,此时y0=64,
∴点C的坐标为(17,64).
(3)①证明:设点P的坐标为(x1,y1),点Q为(x2,y2),(其中x1<1<x2,y1>0,y2>0),
由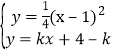 ,得:x2﹣(4k+2)x+4k﹣15=0,
,得:x2﹣(4k+2)x+4k﹣15=0,
∴![]() ,
,
∴(x1﹣1)(x2﹣1)=﹣16,
如图2,分别过点P、Q作x轴的垂线,垂足分别为M、N,
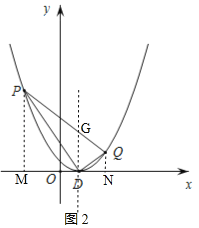
则PM=y1=![]() (x1﹣1)2,QN=y2=
(x1﹣1)2,QN=y2=![]() (x2﹣1)2,
(x2﹣1)2,
DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1,
∴PMQN=DMDN=16,
∴![]() =
=![]() ,
,
又∠PMD=∠DNQ=90°,
∴△PMD∽△DNQ,
∴∠MPD=∠NDQ,
而∠MPD+∠MDP=90°,
∴∠MDP+∠NDQ=90°,即∠PDQ=90°;
②过点D作x轴的垂线交直线PQ于点G,则点G的坐标为(1,4),
所以DG=4,
∴S△PDQ=![]() DGMN=
DGMN=![]() ×4×|x1﹣x2|=2
×4×|x1﹣x2|=2![]() =8
=8![]() ,
,
∴当k=0时,S△PDQ取得最小值16.
-
科目: 来源: 题型:
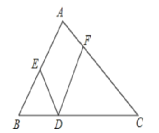
查看答案和解析>>【题目】如图所示,在△ABC中,点D. E. F分别在BC、AB、AC上,且BD=BE,CD=CF,∠EDF=50°.则∠A的度数为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,E、F分别为线段AB、AC上的点(不与A、B、C重合).
(1)如图1,若EF∥BC,求证:
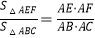
(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若EF上一点G恰为△ABC的重心,
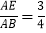 ,求
,求 的值.
的值.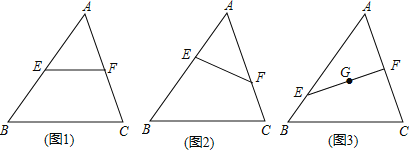
-
科目: 来源: 题型:
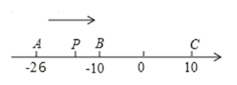
查看答案和解析>>【题目】已知数轴上有 A、B、C 三点,分别表示有理数-26,-10,10,动点 P 从 A 出发,以每秒 1 个 单位的速度向终点 C 移动,设点 P 移动时间为 t 秒.
(1)用含 t 的代数式表示 P 到点 A 和点C 的距离:PA= ,PC=
(2)当点 P 运动到 B 点时,点 Q 从 A 点出发,以每秒 3 个单位的速 度向 C 点运动,Q 点到达 C 点后,再立即以同样的速度返回,当点 P 运动到点 C 时,P、Q 两点运动停止,
①当 P、Q 两点运动停止时,求点 P 和点 Q 的距离;
②求当 t 为何值时 P、Q 两点恰好在途中相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
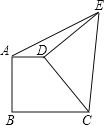
A. 1 B. 2 C. 3 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
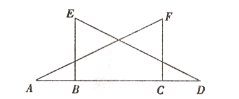
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

相关试题

