【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H. 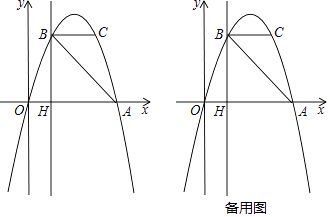
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标.
参考答案:
【答案】
(1)解:把A(4,0),B(1,3)代入y=ax2+bx得 ![]() ,解得
,解得 ![]() ,
,
所以抛物线解析式为y=﹣x2+4x
(2)解:当y=3时,﹣x2+4x=3,解得x1=1,x2=3,则C点坐标为(3,3),
所以△ABC的面积= ![]() ×2×3=3
×2×3=3
(3)解:作PQ⊥BH,如图,设P(m,﹣m2+4m)
∵S△ABH+S梯形APQH=S△PBQ+S△ABP,
∴ ![]() ×3×3+
×3×3+ ![]() (3+m﹣1)×(m2﹣4m)=
(3+m﹣1)×(m2﹣4m)= ![]() ×(m﹣1)×(3+m2﹣4m)+6,
×(m﹣1)×(3+m2﹣4m)+6,
整理得m2﹣5m=0,解得m1=0(舍去),m2=5,
∴P点坐标为(5,﹣5).
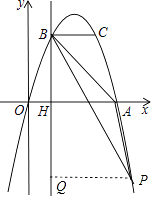
【解析】(1)把A点和B点坐标分别代入y=ax2+bx中得到关于a、b的方程组,然后解方程组即可得到抛物线解析式;(2)计算函数值为3所对应的自变量的值即可得到C点,然后根据三角形面积公式计算△ABC的面积;(3)作PQ⊥BH,如图,设P(m,﹣m2+4m),则利用S△ABH+S梯形APQH=S△PBQ+S△ABP可得到关于m的方程,然后解方程求出m即可得到P点坐标.
【考点精析】本题主要考查了二次函数图象的平移和抛物线与坐标轴的交点的相关知识点,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一次函数y=ax+b(a≠0)的图象与反比例函数y=
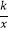 (k≠0)的图象交于M,N两点.
(k≠0)的图象交于M,N两点. 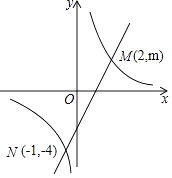
(1)求反比例函数与一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
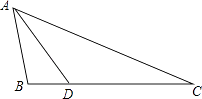
(1)求证:△ABD∽△CBA;
(2)若DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和
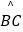 的长分别为( )
的长分别为( ) 
A.2,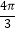
B.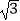 ,π
,π
C.2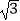 ,
, 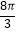
D.2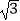 ,
, 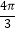
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=﹣
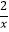 ,下列结论不正确的是( )
,下列结论不正确的是( )
A.图象必经过点(﹣1,2)
B.y随x的增大而增大
C.图象在第二、四象限内
D.若x>1,则y>﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=6,BC=4,将△ABC绕点A逆时针旋转得到△AEF,使得AF∥BC,延长BC交AE于点D,则线段CD的长为( )
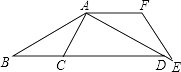
A.4
B.5
C.6
D.7
相关试题

