【题目】已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1. 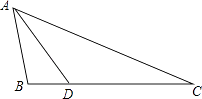
(1)求证:△ABD∽△CBA;
(2)若DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长.
参考答案:
【答案】
(1)证明:∵AB=2,BC=4,BD=1,
∴ ![]() ,
,
∵∠ABD=∠CBA,
∴△ABD∽△CBA
(2)解:∵DE∥AB,
∴△CDE∽△CBA,
∴△ABD∽△CDE,
∴DE=1.5.
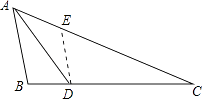
【解析】(1)在△ABD与△CBA中,有∠B=∠B,根据已知边的条件,只需证明夹此角的两边对应成比例即可;(2)由(1)知△ABD∽△CBA,又DE∥AB,易证△CDE∽△CBA,则:△ABD∽△CDE,然后根据相似三角形的对应边成比例得出DE的长.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
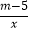 (m为常数,且m≠5).
(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=﹣x+1图象的一个交点的纵坐标是3,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一次函数y=ax+b(a≠0)的图象与反比例函数y=
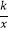 (k≠0)的图象交于M,N两点.
(k≠0)的图象交于M,N两点. 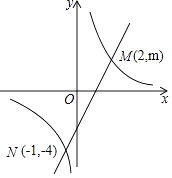
(1)求反比例函数与一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
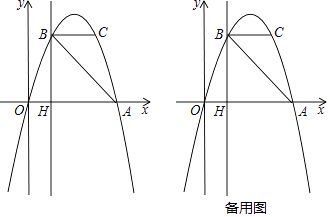
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和
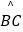 的长分别为( )
的长分别为( ) 
A.2,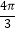
B.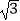 ,π
,π
C.2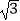 ,
, 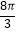
D.2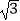 ,
, 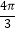
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=﹣
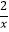 ,下列结论不正确的是( )
,下列结论不正确的是( )
A.图象必经过点(﹣1,2)
B.y随x的增大而增大
C.图象在第二、四象限内
D.若x>1,则y>﹣2
相关试题

