【题目】如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和 ![]() 的长分别为( )
的长分别为( ) 
A.2, ![]()
B.![]() ,π
,π
C.2 ![]() ,
, ![]()
D.2 ![]() ,
, ![]()
参考答案:
【答案】D
【解析】解:如图所示,连接OC、OB, ∵多边形ABCDEF是正六边形,
∴∠BOC=60°,
∵OA=OB,
∴△BOC是等边三角形,
∴∠OBM=60°,
∴OM=OBsin∠OBM=4× ![]() =2
=2 ![]() ,
,![]() 的长=
的长= ![]() =
= ![]() ;
;
故选:D.
【考点精析】解答此题的关键在于理解正多边形和圆的相关知识,掌握圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等,以及对弧长计算公式的理解,了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一次函数y=ax+b(a≠0)的图象与反比例函数y=
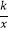 (k≠0)的图象交于M,N两点.
(k≠0)的图象交于M,N两点. 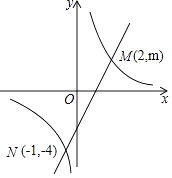
(1)求反比例函数与一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
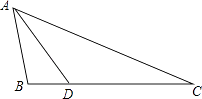
(1)求证:△ABD∽△CBA;
(2)若DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
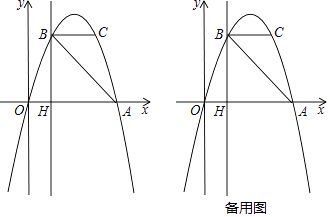
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=﹣
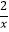 ,下列结论不正确的是( )
,下列结论不正确的是( )
A.图象必经过点(﹣1,2)
B.y随x的增大而增大
C.图象在第二、四象限内
D.若x>1,则y>﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=6,BC=4,将△ABC绕点A逆时针旋转得到△AEF,使得AF∥BC,延长BC交AE于点D,则线段CD的长为( )
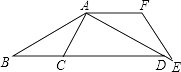
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y1=mx(m>0)的图象与反比例函数y2=
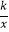 (k≠0)的图象交于点A(n,4)和点B,AM⊥y轴,垂足为M.若△AMB的面积为8,则满足y1>y2的实数x的取值范围是 .
(k≠0)的图象交于点A(n,4)和点B,AM⊥y轴,垂足为M.若△AMB的面积为8,则满足y1>y2的实数x的取值范围是 .
相关试题

