【题目】定义:(ⅰ)如果两个函数![]() ,存在
,存在 ![]() 取同一个值,使得
取同一个值,使得![]() ,那么称
,那么称 ![]() 为“互联互通函数”,称对应的
为“互联互通函数”,称对应的![]() 值为
值为![]() 的“互联点”; (ⅱ)如果两个函数
的“互联点”; (ⅱ)如果两个函数![]() 为“互联互通函数”,那么
为“互联互通函数”,那么![]() 的最大值称为
的最大值称为![]() 的“互通值”.
的“互通值”.
(1)判断函数![]() 与
与![]() 是否为“互通互联函数”,如果是,请求出
是否为“互通互联函数”,如果是,请求出![]() 时他们的“互联点”,如果不是,请说明理由;
时他们的“互联点”,如果不是,请说明理由;
(2)当![]() 时,已知函数
时,已知函数![]() 与
与![]() 是“互联互通函数”.且有唯一“互联点”;
是“互联互通函数”.且有唯一“互联点”;
①求出![]() 的取值范围;
的取值范围;
②若他们的“互通值”为18 ,试求出 ![]() 的值.
的值.
参考答案:
【答案】(1)![]() 与
与![]() 是互联互通函数,互联点为
是互联互通函数,互联点为![]() 与
与![]() ;(2)①当
;(2)①当![]() 或
或![]() 时,②
时,②![]() 的值为
的值为![]() 或3
或3
【解析】
(1)联立解析式消去y,得到关于x的方程,若方程有实根则这两个函数为“合作函数”;把m=2代入函数,联立解析式求出x的值即为合作点;
(2)①当![]() 时,求出m的值,当
时,求出m的值,当![]() 时是互联互通函数,即可求出x,y的值,即可解答
时是互联互通函数,即可求出x,y的值,即可解答
②共赢点即为![]() 的最大值,而
的最大值,而![]() 是二次函数且开口向上,所以最大值在端点求得,分别将
是二次函数且开口向上,所以最大值在端点求得,分别将![]() 或
或![]() 代入解析式求出最大值等于18,得到关于m的方程求解即可。
代入解析式求出最大值等于18,得到关于m的方程求解即可。
(1)依题意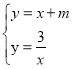
∴![]()
∴![]()
∴![]() ,即两函数有交点
,即两函数有交点
∴![]() 与
与![]() 为互联互通函数
为互联互通函数
当![]() 时,
时,![]()
∴![]()
∴互联点为![]() 与
与![]()
(2)①当![]() 时,
时,
![]() ∴
∴![]()
∴当![]() 时是互联互通函数,
时是互联互通函数,![]()
即互联点为![]()
当![]() 或
或![]() 时,不是“互联互通函数”
时,不是“互联互通函数”
②依题意,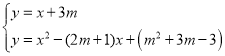
∴![]()
∴![]()
![]()
![]()
∴![]() 或
或![]()
当![]() 或
或![]() 时,
时,![]()
![]()
![]()
![]() (舍)
(舍)
当![]() 时,
时,![]()
![]() (舍)
(舍)![]()
∴![]() 的值为
的值为![]() 或3
或3
-
科目: 来源: 题型:
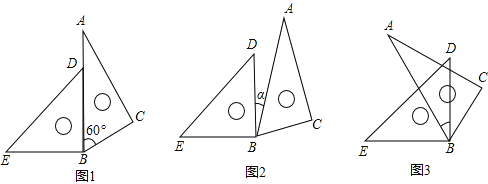
查看答案和解析>>【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小宇在周日上午8:00从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心
接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/时的平均速
度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原
路返回.设小宇离家 x 小时后,到达离家y千米的地方,图中折线OABCD表示 y 与 x 之间的函数关系.下
列叙述错误的是( )
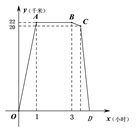
A. 活动中心与小宇家相距22千米
B. 小宇在活动中心活动时间为2小时
C. 他从活动中心返家时,步行用了0.4小时
D. 小宇不能在12:00前回到家
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
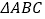 中,
中,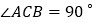 ,点
,点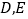 分别是
分别是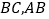 上的中点,连接
上的中点,连接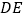 并延长至点
并延长至点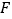 ,使
,使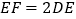 ,连接
,连接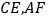 .
.(1)证明:
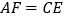 ;
;(2)若
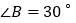 ,AC=2,连接BF,求BF的长
,AC=2,连接BF,求BF的长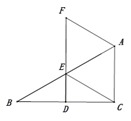
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、BF分别是⊙O的直径和弦,弦CD与AB、BF分别相交于点E、G,过点F的切线HF与DC的延长线相交于点H,且HF=HG.
(1)求证:AB⊥CD;
(2)若sin∠HGF=
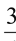 ,BF=3,求⊙O的半径长.
,BF=3,求⊙O的半径长.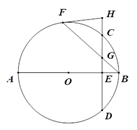
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B. C,与y轴的负半轴相交于D,抛物线y=x
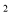 +bx+c经过B. C. D三点。
+bx+c经过B. C. D三点。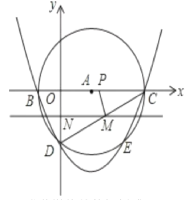
(1)求此抛物线的解析式;
(2)若动直线MN(MN∥x轴)从点D开始,以每秒1个长度单位的速度沿y轴的正方向移动,且与线段CD、y轴分别交于M、N两点,动点P同时从点C出发,在线段OC上以每秒2个长度单位的速度向原点O运动,连接PM,设运动时间为t秒,若以P、C. M为顶点的三角形与△OCD相似,求实数t的值;
②当t为何值时,
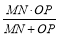 的值最大,并求出最大值。
的值最大,并求出最大值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下,请补充完整.
收集数据 17 18 16 12 24 15 27 25 18 19
22 17 16 19 31 29 16 14 15 25
15 31 23 17 15 15 27 27 16 19
整理、描述数据
销售额/万元
12
14
15
16
17
18
19
22
23
24
25
27
29
31
人数
1
1
4
3
2
1
1
1
2
3
1
2
分析数据 样本数据的平均数、众数、中位数如下表所示:
平均数
众数
中位数
20
18
得出结论 ⑴如果想让一半左右的营业员都能达到销售目标,你认为月销售额应定为 万元.
⑵如果想确定一个较高的销售目标,这个目标可以定为每月 万元,理由为 .
相关试题

