搜索
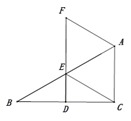
【题目】如图，在
中，
，点
分别是
上的中点，连接
并延长至点
，使
，连接
.
（1）证明：
；
（2）若
，AC=2，连接BF，求BF的长
参考答案：
【答案】(1)见解析；（2）
【解析】试题分析：（1）由三角形中位线定理得出DE∥AC，AC=2DE,求出EF∥AC，
，得出四边形
是平行四边形，即可得出
；
解三角形求出
的长度，在
中用勾股定理即可求出BF的长.
试题解析：（1）∵D，E分别是BC，AB上的中点,
∴DE为△ABC的中位线,
∴DE∥AC，AC=2DE,
又∵DF=2DE,
∴EF=AC,
∴四边形ACEF为平行四边形,
∴AF=CE.
（2）∵∠ABC=90°，∠B=30°，AC=2,
∴
∵D为BC中点
∴
又∵EF=2DE,
∴EF=2,
∴DF=3,
在△BDF中，由勾股定理得
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】把一根绳子对折成一条线段AB，在线段AB取一点P，使AP＝
，从P处把绳子剪断，若剪断后的三段绳子中最长的一段为30cm，则绳子的原长为______cm． -
科目： 来源： 题型：
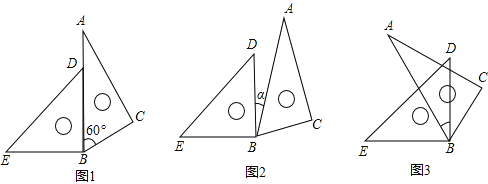
查看答案和解析>>【题目】（1）平面内将一副三角板按如图1所示摆放，∠EBC= °；
（2）平面内将一副三角板按如图2所示摆放，若∠EBC=165°，那么∠α= °；
（3）平面内将一副三角板按如图3所示摆放，∠EBC=115°，求∠α的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小宇在周日上午8：00从家出发，乘车1小时到达某活动中心参加实践活动．11：00时他在活动中心
接到爸爸的电话，因急事要求他在12：00前回到家，他即刻按照来活动中心时的路线，以5千米/时的平均速
度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原
路返回．设小宇离家 x 小时后，到达离家y千米的地方，图中折线OABCD表示 y 与 x 之间的函数关系．下
列叙述错误的是（ ）
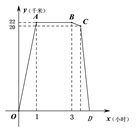
A. 活动中心与小宇家相距22千米
B. 小宇在活动中心活动时间为2小时
C. 他从活动中心返家时，步行用了0.4小时
D. 小宇不能在12：00前回到家
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：（ⅰ）如果两个函数
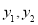，存在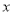 
取同一个值，使得
，那么称 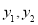为“互联互通函数”，称对应的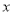值为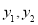 的“互联点”； （ⅱ）如果两个函数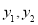为“互联互通函数”，那么
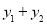的最大值称为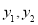的“互通值”.（1）判断函数
与
是否为“互通互联函数”，如果是，请求出
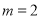时他们的“互联点”，如果不是，请说明理由；（2）当
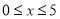时，已知函数与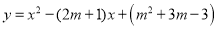
是“互联互通函数”.且有唯一“互联点”；①求出
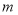的取值范围；②若他们的“互通值”为18 ，试求出
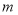的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB、BF分别是⊙O的直径和弦，弦CD与AB、BF分别相交于点E、G，过点F的切线HF与DC的延长线相交于点H，且HF＝HG.
（1）求证：AB⊥CD；
（2）若sin∠HGF＝
，BF＝3，求⊙O的半径长.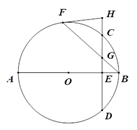
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B. C,与y轴的负半轴相交于D,抛物线y=x
+bx+c经过B. C. D三点。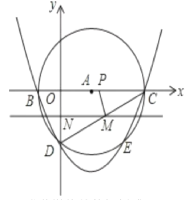
(1)求此抛物线的解析式；
(2)若动直线MN(MN∥x轴)从点D开始，以每秒1个长度单位的速度沿y轴的正方向移动，且与线段CD、y轴分别交于M、N两点，动点P同时从点C出发，在线段OC上以每秒2个长度单位的速度向原点O运动，连接PM，设运动时间为t秒，若以P、C. M为顶点的三角形与△OCD相似，求实数t的值；
②当t为何值时,
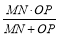的值最大，并求出最大值。
相关试题
