【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).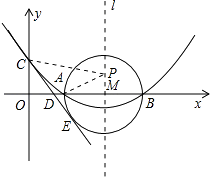
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
参考答案:
【答案】
(1)
解:由题意,设抛物线的解析式为y=a(x﹣4)2﹣ ![]() (a≠0)
(a≠0)
∵抛物线经过(0,2)
∴a(0﹣4)2﹣ ![]() =2
=2
解得:a= ![]()
∴y= ![]() (x﹣4)2﹣
(x﹣4)2﹣ ![]()
即:y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
当y=0时, ![]() x2﹣
x2﹣ ![]() x+2=0
x+2=0
解得:x=2或x=6
∴A(2,0),B(6,0)
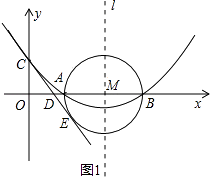
(2)
解:存在,
如图2,由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=2 ![]() ,
,
∴AP+CP=BC=2 ![]()
∴AP+CP的最小值为2 ![]()
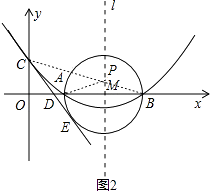
(3)
解:如图3,连接ME
∵CE是⊙M的切线
∴ME⊥CE,∠CEM=90°
∵C的坐标(0,2),
∴OC=2,
∵AB=4,
∴ME=2
∴OC=ME=2,
∵∠ODC=∠MDE,
∵在△COD与△MED中
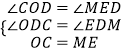
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM
设OD=x
则CD=DM=OM﹣OD=4﹣x
则Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4﹣x)2
∴x= ![]()
∴D( ![]() ,0)
,0)
设直线CE的解析式为y=kx+b(k≠0),
∵直线CE过C(0,2),D( ![]() ,0)两点,
,0)两点,
则 
解得: 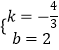
∴直线CE的解析式为y=﹣ ![]() +2;
+2;

【解析】(1)利用顶点式求得二次函数的解析式后令其等于0后求得x的值即为与x轴交点坐标的横坐标;(2)线段BC的长即为AP+CP的最小值;(3)连接ME,根据CE是⊙M的切线得到ME⊥CE,∠CEM=90°,从而证得△COD≌△MED,设OD=x,在RT△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB. 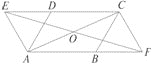
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正偶数从小到大排列,并按如下规律分组:
第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A10=(2,3),则A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,……,按如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中D的位置是有理数( ),2008应排在A、B、C、D、E中的( ) 位置.其中两个填空依次为( )

A. 29,C B. ﹣29,D C. 30,B D. ﹣31,E
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒时其中一个四边形为平行四边形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )

A.πcm2
B. πcm2
πcm2
C. cm2
cm2
D. cm2
cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后,将三角形纸片①绕AB的中点O旋转至三角形纸片②处,以此方法继续操作,即可拼成一个新的正方形DEFG.




请你参考小明的做法解决下列问题:
(1)现有5个形状,大小相同的矩形纸片,排列形式如图3所示.请将其分割后拼接成一个平行四边形,要求:在图3中画出并指明拼接成的平行四边形(画出一个符合条件的平行四边形即可).
(2)如图4,在面积为2的平行四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,分别连结AF、BG、CH、DE,所得□MNPQ面积为__________.
相关试题

