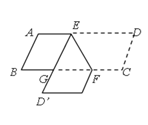
【题目】如图,在□ABCD中,点E,F分别在边AD、BC上,EF=2,∠DEF=60°将四边形EFCD沿EF翻折,得到四边形EFC’D’,ED’交BC于点G,则△GEF的周长为________.
参考答案:
【答案】6;
【解析】分析:根据平行四边形的性质得到AD∥BC,由平行线的性质得到∠AEG=∠EGF,根据折叠的性质得到∠GEF=∠DEF=60°,推出△EGF是等边三角形,于是得到结论.
详解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEG=∠EGF,
∵将四边形EFCD沿EF翻折,得到EFC′D′,
∴∠GEF=∠DEF=60°,
∴∠AEG=60°,
∴∠EGF=60°,
∴△EGF是等边三角形,
∵EF=2,
∴△GEF的周长=6,
故答案为6.
题睛:本题考查了翻折变换的性质、平行四边形的性质、等边三角形的判定,熟练掌握翻折变换的性质是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.
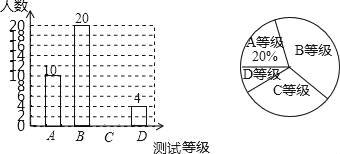
请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了 名学生?测试结果为C等级的学生数是 ,并补全条形图;
(2)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两名恰好都是男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式2x3y﹣xy+16的次数为a,常数项为b,a,b分别对应着数轴上的A、B两点.
(1)a= ,b= ;并在数轴上画出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度单位的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动的终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.

-
科目: 来源: 题型:
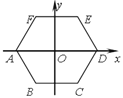
查看答案和解析>>【题目】如图,正六边形 ABCDEF的中心与坐标原点O重合,其中A(-2,0).将六边形 ABCDEF绕原点O按顺时针方向旋转2018次,每次旋转60°,则旋转后点A的对应点A'的坐标是( ).
A. (1,
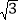 ) B. (
) B. (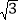 ,1) C. (1,
,1) C. (1,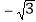 ) D. (-1,
) D. (-1,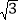 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y=
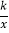 (x>0)经过A、B两点,若点A的横坐标为1,∠OAB=90°,且OA=AB,则k的值为________.
(x>0)经过A、B两点,若点A的横坐标为1,∠OAB=90°,且OA=AB,则k的值为________.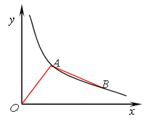
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任到一点P(点A除外),过点P作EF∥AB,分别交AC、BC于点E、F,作PQ∥AC,交AB于点Q,连接QE与AD相交于点G.
(1)求证:四边形AQPE是菱形.
(2)四边形EQBF是平行四边形吗?若是,请证明;若不是,请说明理由.
(3)直接写出P点在EF的何处位置时,菱形AQPE的面积为四边形EQBF面积的一半.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 是
是 的中点,
的中点, 是
是 的中点,过点
的中点,过点 作
作 交
交 的延长线于点
的延长线于点 ,连接
,连接 .
.
(1)写出四边形
 的形状,并证明:
的形状,并证明:(2)若四边形
 的面积为12,
的面积为12, ,求
,求 .
.
相关试题

