【题目】阅读以下内容并回答问题:
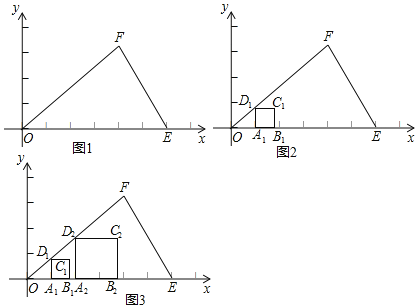
如图1,在平面直角坐标系xOy中,有一个△OEF,要求在△OEF内作一个内接正方形ABCD,使正方形A,B两个顶点在△OEF的OE边上,另两个顶点C,D分别在EF和OF两条边上.
小丽感到要使四边形的四个顶点同时满足上述条件有些困难,但可以先让四边形的三个顶点满足条件,于是她先画了一个有三个顶点在三角形边上的正方形(如图2).接着她又在△OEF内画了一个这样的正方形(如图3).她发现如果再多画一些这样的正方形,就能发现这些点C位置的排列图形,根据这个图形就能画出满足条件的正方形了.
(1)请你也实验一下,再多画几个这样的正方形,猜想小丽发现这些点C排列的图形是 ;
(2)请你参考上述思路,继续解决问题:如果E,F两点的坐标分别为E(6,0),F(4,3).
①当A1的坐标是(1,0)时,则C1的坐标是 ;
②当A2的坐标是(2,0)时,则C2的坐标是 ;
③结合(1)中猜想,求出正方形ABCD的顶点D的坐标,在图3中画出满足条件的正方形ABCD.
参考答案:
【答案】(1)一条线段;(2)①(![]() ,
,![]() );②(
);②(![]() ,
,![]() );D点坐标为(
);D点坐标为(![]() ,2),③见解析.
,2),③见解析.
【解析】
(1)通过画图,可直接得出结论;
(2)先确定出直线OF的解析式,
①将x=1代入直线OF解析式求出y,即可得出结论;
②将x=2代入直线OF解析式求出y,即可得出结论;
③先求出直线C1C2的表达式为y=![]() x和直线EF的表达式为y=﹣
x和直线EF的表达式为y=﹣![]() +9,进而求出C点坐标为(
+9,进而求出C点坐标为(![]() ,2),即可得出结论.
,2),即可得出结论.
解:(1)通过画图,猜想小丽发现这些点C排列的图形是一条线段;
故答案为:一条线段;
(2)∵F(4,3).
∴直线OF的表达式是y=![]() x,
x,
①∵四边形A1B1C1D1是正方形,
∴A1D1=A1B1,
把x=1代入直线y=![]() x中,得y=
x中,得y=![]() ,
,
∴OB1=OA1+A1B1=1+![]() =
=![]() ,
,
∴C1的坐标是 (![]() ,
,![]() ),
),
故答案为:(![]() ,
,![]() );
);
②∵四边形A2B2C2D2是正方形,
∴A2D2=A2B2,
把x=2代入直线y=![]() x中,得y=
x中,得y=![]() ,
,
∴OB2=OA2+A2B2=2+![]() =
=![]() ,
,
∴C2的坐标是 (![]() ,
,![]() ),
),
故答案为:(![]() ,
,![]() );
);
③设过C1,C2两点的一次函数表达式是y=kx+b(k≠0).
代入C1,C2两点得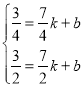 ,
,
解得![]() ,
,
∴直线C1C2的表达式为y=![]() x,
x,
设过E(6,0),F(4,3)两点的一次函数表达式是y=k'x+b'(k'≠0).
代入E,F两点得![]()
解得 ,
,
所以直线EF的表达式为y=﹣![]() x+9
x+9
直线EF:y=﹣![]() x+9与直线C1C2:y=
x+9与直线C1C2:y=![]() x的交点坐标为C.
x的交点坐标为C.
联立直线EF和直线C1C2解析式成方程组并求解得:x=![]() ,y=2.
,y=2.
∴C点坐标为(![]() ,2).
,2).
把y=2代入y=![]() x,解得x=
x,解得x=![]() ,
,
∴D点坐标为(![]() ,2)
,2)
所画四边形ABCD如图3所示,

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 年
年 月
月 日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,我校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列统计图(说明:A级:90分——100分;B级:75分——89分;C级:60分——74分;D级:60分以下).请结合图中提供的信息,解答下列问题:
日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,我校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列统计图(说明:A级:90分——100分;B级:75分——89分;C级:60分——74分;D级:60分以下).请结合图中提供的信息,解答下列问题: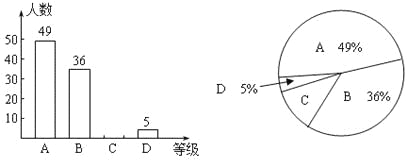
(1)扇形统计图中C级所在的扇形的圆心角度数是 .
(2)请把条形统计图补充完整;
(3)若该校共有2000名学生,请你用此样本估计安全知识竞赛中A级和B级的学生共约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
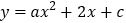 的图象经过点
的图象经过点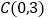 ,与
,与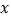 轴分别交于点
轴分别交于点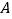 ,点
,点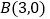 .点
.点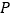 是直线
是直线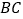 上方的抛物线上一动点.
上方的抛物线上一动点.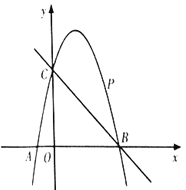
(1)求二次函数
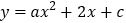 的表达式;
的表达式;(2)连接
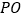 ,
,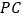 ,并把
,并把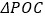 沿
沿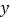 轴翻折,得到四边形
轴翻折,得到四边形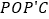 .若四边形
.若四边形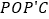 为菱形,请求出此时点
为菱形,请求出此时点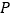 的坐标;
的坐标;(3)当点
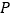 运动到什么位置时,四边形
运动到什么位置时,四边形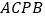 的面积最大?求出此时
的面积最大?求出此时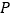 点的坐标和四边形
点的坐标和四边形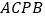 的最大面积.
的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知第一象限内的点A在反比例函数y=
 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=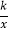 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA= ,则k的值为( )
,则k的值为( )
A. -3 B. -6 C. -4 D. -
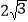
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
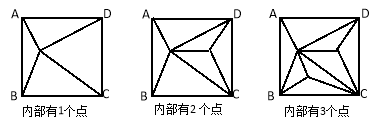
(1)填写下表:
正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有_____.(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).
问:(1)设购买乒乓球x盒时,在甲家购买所需多少元?在乙家购买所需多少元?(用含x的代数式表示,并化简)
(2)当购买乒乓球多少盒时,两种优惠办法付款一样?
相关试题

