【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有_____.(填序号)

参考答案:
【答案】①②③④
【解析】分析:分别利用平行线的性质结合线段垂直平分线的性质以及等腰三角形的性质分别判断得出答案.
详解:∵BC=EC,
∴∠CEB=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CEB=∠EBF,
∴∠CBE=∠EBF,
∴①BE平分∠CBF,正确;
∵BC=EC,CF⊥BE,
∴∠ECF=∠BCF,
∴②CF平分∠DCB,正确;
∵DC∥AB,
∴∠DCF=∠CFB,
∵∠ECF=∠BCF,
∴∠CFB=∠BCF,
∴BF=BC,
∴③正确;
∵FB=BC,CF⊥BE,
∴B点一定在FC的垂直平分线上,即PB垂直平分FC,
∴PF=PC,故④正确.
故答案为①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)先化简,再求值:( ﹣
﹣  )
)  ,其中x=
,其中x=  ﹣2.
﹣2.
(2)计算:|﹣4|+( )﹣2﹣(
)﹣2﹣(  ﹣1)0﹣
﹣1)0﹣ 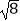 cos45°.
cos45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面上四点A,B,C,D,按下列要求画出图形;
(1)射线AB,直线CB;
(2)取线段AB的中点E,连接DE并延长与直线CB交于点O;
(3)在所画的图形中,若AB=6,BE=BC=
 OB,求OC的长.
OB,求OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会主席换届选举,经初选、复选后,共有甲,乙,丙三人进入最后的竞选,最后决定用投票方式进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开票,结果如表所示:
 单位:票
单位:票
投票箱
候选人
废票
合计
甲
乙
丙
一
200
211
147
12
570
二
244
15
630
三
97
41
205
7
350
四
250
 若第二投票箱候选人甲的得票数比乙的3倍还多31票,请分别求出第二投票箱甲、乙两名候选人的得票数.
若第二投票箱候选人甲的得票数比乙的3倍还多31票,请分别求出第二投票箱甲、乙两名候选人的得票数. 根据
根据 题的数据分析,请判断乙侯选人是否还有机会当选,并详细解释或完整写出你的解题过程.
题的数据分析,请判断乙侯选人是否还有机会当选,并详细解释或完整写出你的解题过程. -
科目: 来源: 题型:
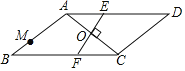
查看答案和解析>>【题目】如图,在ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为______.
相关试题

