【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图象与过
的图象与过![]() 、
、![]() 的直线交于点P,与x轴、y轴分别相交于点C和点D.
的直线交于点P,与x轴、y轴分别相交于点C和点D.
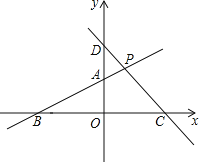
![]() 求直线AB的解析式及点P的坐标;
求直线AB的解析式及点P的坐标;
![]() 连接AC,求
连接AC,求![]() 的面积;
的面积;
![]() 设点E在x轴上,且与C、D构成等腰三角形,请直接写出点E的坐标.
设点E在x轴上,且与C、D构成等腰三角形,请直接写出点E的坐标.
参考答案:
【答案】(1)![]() ,,P
,,P![]() (2)
(2)![]() ;(3)点E的坐标为
;(3)点E的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)由点A、B的坐标,利用待定系数法即可求出直线AB的解析式,再联立直线AB、CD的解析式成方程组,通过解方程组可求出点P的坐标;
(2)过点P作PM⊥BC于点M,利用一次函数图象上点的坐标特征可求出点C的坐标,结合点A、B、P的坐标,可得出BC、OA、PM的值,利用三角形的面积公式结合S△PAC=S△PBC-S△ABC即可求出△PAC的面积;
(3)利用一次函数图象上点的坐标特征可得出点C、D的坐标,进而可得出CD的长度,分DE=DC、CD=CE、EC=ED三种情况求出点E的坐标,此题得解.
![]() 设直线AB的解析式为
设直线AB的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() ,得:
,得:
![]() ,解得:
,解得:
![]() 直线AB的解析式为
直线AB的解析式为![]() .
.
联立直线AB、CD的解析式成方程组,得:
 ,解得:
,解得: ,
,
![]() 点P的坐标为
点P的坐标为![]()
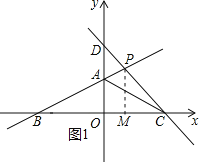
![]() 过点P作
过点P作![]() 于点M,如图1所示.
于点M,如图1所示.
![]() 点P的坐标为
点P的坐标为![]() ,
,
![]() .
.
![]() 一次函数
一次函数![]() 的图象与x轴交于点C,
的图象与x轴交于点C,
![]() 点C的坐标为
点C的坐标为![]() ,
,
![]() .
.
![]() 点A的坐标为
点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
 .
.
![]() 为等腰三角形,
为等腰三角形,
![]() 或
或![]() 或
或![]() 如图
如图![]() .
.
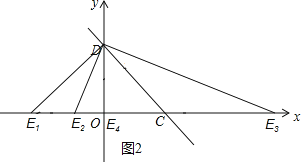
![]() 一次函数
一次函数![]() 的图象与x轴、y轴分别相交于点C和点D,
的图象与x轴、y轴分别相交于点C和点D,
![]() 点C的坐标为
点C的坐标为![]() ,点D的坐标为
,点D的坐标为![]() ,
,
![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 点E的坐标为
点E的坐标为![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
![]() 点E的坐标为
点E的坐标为![]() 或
或![]() ;
;
![]() 当
当![]() 时,点E与点O重合,
时,点E与点O重合,
![]() 点E的坐标为
点E的坐标为![]() .
.
综上所述:点E的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
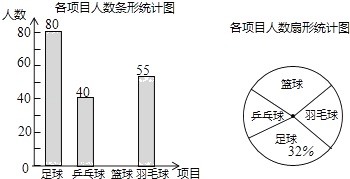
(1)这次活动一共调查了名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是人. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+m的图象与反比例函数y=
 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
 求A种,B种树木每棵各多少元?
求A种,B种树木每棵各多少元? 因布局需要,购买A种树木的数量不少于B种树木数量的3倍
因布局需要,购买A种树木的数量不少于B种树木数量的3倍 学校与中标公司签订的合同中规定:在市场价格不变的情况下
学校与中标公司签订的合同中规定:在市场价格不变的情况下 不考虑其他因素
不考虑其他因素 ,实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,
,实际付款总金额按市场价九折优惠,请设计一种购买树木的方案, -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )
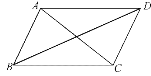
A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们可以将任意三位数表示为
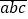 (其中a、b、c 分别表示百位上的数字,十位上的数字和个位上的数字,且a
(其中a、b、c 分别表示百位上的数字,十位上的数字和个位上的数字,且a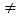 0)显然,
0)显然,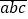 = 100a+10b+c;我们把形如
= 100a+10b+c;我们把形如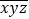 和
和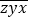 的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对“姊妹数”,789和987是一对“姊妹数”.
的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对“姊妹数”,789和987是一对“姊妹数”.(1)一对“姊妹数”的和为1110,求这对“姊妹数”.
(2)如果用x表示百位数字,试说明:任意一对“姊妹数”的和能被37整除.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、并三位同学参加数学综合素质测试
 各项成绩如下
各项成绩如下 单位:分
单位:分
同学
成绩
数与代数
图形与几何
统计与概率
综合与实践
甲
90
93
89
90
乙
94
92
94
86
丙
92
91
90
88
 甲、乙、丙三位同学成绩的中位数分别为______;
甲、乙、丙三位同学成绩的中位数分别为______; 如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
相关试题

