搜索
【题目】甲、乙、并三位同学参加数学综合素质测试
各项成绩如下
单位：分
同学 成绩 | 数与代数 | 图形与几何 | 统计与概率 | 综合与实践 |
甲 | 90 | 93 | 89 | 90 |
乙 | 94 | 92 | 94 | 86 |
丙 | 92 | 91 | 90 | 88 |
甲、乙、丙三位同学成绩的中位数分别为______；
如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3：3：2：2计算，分别计算甲、乙、丙三位同学的数学综合素质测试成绩，从成绩看，应推荐谁参加更高级别的比赛？
参考答案：
【答案】
90分、93分、
分；
从成绩看，应推荐乙参加更高级别的比赛
【解析】
根据中位数的定义分别计算可得；
根据加权平均数的定义列式计算可得．
由表可知，甲的中位数为
分，乙的中位数为
分，丙的中位数为
分，
故答案为：90分、93分、分；
甲的平均成绩为
分，
乙的平均成绩为
分，
丙的平均成绩为
分，
所以，从成绩看，应推荐乙参加更高级别的比赛．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知一次函数
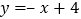的图象与过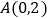
、
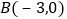的直线交于点P，与x轴、y轴分别相交于点C和点D．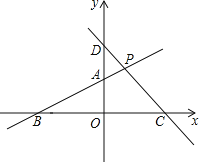
求直线AB的解析式及点P的坐标；
连接AC，求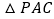
的面积；
设点E在x轴上，且与C、D构成等腰三角形，请直接写出点E的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四边形ABCD是平行四边形，则下列结论中不正确的是( )
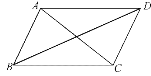
A. 当AB＝BC时，四边形ABCD是菱形
B. 当AC⊥BD时，四边形ABCD是菱形
C. 当∠ABC＝90°时，四边形ABCD是矩形
D. 当AC＝BD时，四边形ABCD是正方形
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们可以将任意三位数表示为
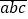（其中a、b、c 分别表示百位上的数字，十位上的数字和个位上的数字，且a
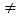0）显然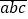，= 100a+10b+c；我们把形如
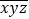和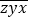
的两个三位数称为一对“姊妹数”（其中x、y、z是三个连续的自然数）如：123和321是一对“姊妹数”,789和987是一对“姊妹数”.（1）一对“姊妹数”的和为1110，求这对“姊妹数”.
（2）如果用x表示百位数字，试说明：任意一对“姊妹数”的和能被37整除.
-
科目： 来源： 题型：
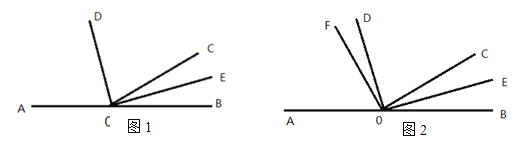
查看答案和解析>>【题目】如图1，已知A、O、B三点在同一直线上，射线OD、OE分别平分∠AOC、∠BOC
（1）求∠DOE的度数；
（2）如图2，在∠AOD内引一条射线OF，使∠COF=
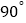，其他不变，设∠DOF=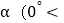
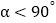）①求∠AOF的度数（用含
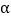的代数式表示）.②若∠BOD是∠AOF的2倍，求∠DOF的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在矩形纸片ABCD中，AB=3cm，AD=5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．
（1）求证：四边形BFEP为菱形；
（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；
①当点Q与点C重合时（如图2），求菱形BFEP的边长；
②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上三点M，O，N对应的数分别为－1，0，3，点P为数轴上任意一点，其对应的数为x．
（1）MN的长为 ；
（2）如果点P到点M、点N的距离相等，那么x的值是 ；
（3）数轴上是否存在点P，使点P到点M、点N的距离之和是8？若存在，直接写出x的值；若不存在，请说明理由．
（4）如果点P以每分钟1个单位长度的速度从点O向左运动，同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动．设t分钟时点P到点M、点N的距离相等，求t的值．
相关试题
