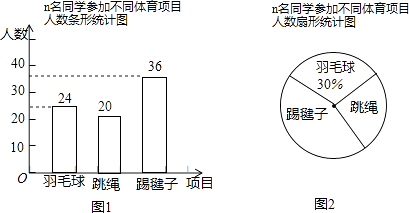
【题目】为加强学生课间锻炼，某校决定开设羽毛球、跳绳、踢毽子三种运动项目，为了解学生最喜欢哪一种项目，随机抽取了n名学生进行调查（每名同学选择一种体育项目），并将调查结果绘制成如图两个统计图．
请结合上述信息解答下列问题：
（1）求n的值；
（2）请把条形统计图补充完整；
（3）已知该校有1200人，请你根据统计图中的资料估计全校最喜欢踢毽子的人数．

参考答案：

【答案】
（1）解：n= =80（名）；
（2）解：最喜欢参加跳绳的人数=80﹣24﹣36=20（名），

画条形统计图如下：


（3）解：∵1200× =540，

∴估计全校最喜欢踢毽子的人数为540人．


【解析】（1）根据两个统计图得到最喜欢参加羽毛球占30%，而最喜欢参加羽毛球的人数为24，然后用24除以30%即可得到n的值；（2）先计算出最喜欢参加跳绳的人数，然后补全统计图；（3）先计算出最喜欢踢毽子的百分比，然后用1200乘以这个百分比就可估计出全校最喜欢踢毽子的人．
【考点精析】通过灵活运用扇形统计图和条形统计图，掌握能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况；能清楚地表示出每个项目的具体数目，但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况即可以解答此题．

关闭