【题目】阅读与思考:整式乘法与因式分解是方向相反的变形
由(x+p)(x+q)=x2+(p+q)x+pq得x2+(p+q)x+pq=(x+p)(x+q)
利用这个式子可以将某些二次项系数是1的二次三项式分解因式,
例如:将式子x2+3x+2分解因式.
分析:这个式子的常数项2=1×2一次项系数3=1+2
所以x2+3x+2=x2+(1+2)x=1×2
解:x2+3x+2=(x+)(x+2)
请仿照上面的方法,解答下列问题:
(1)分解因式:x2+6x-27=__________________;
(2)若x2+px+8可分解为两个一次因式的积,则整数![]() 的所有可能值是_________________;
的所有可能值是_________________;
(3)利用因式分解法解方程:x2-4x-12=0..
参考答案:
【答案】(1)(x-3)(x+9);(2)±9或±6;(3)x=-2或x=6.
【解析】试题分析:(1)利用十字相乘法分解因式即可;
(2)找出所求满足题意p的值即可;
(3)方程利用因式分解法求出解即可.
试题解析:(1)x2+6x-27═(x+9)(x-3),
故答案为:(x+9)(x-3);
(2)∵8=1×8;-8=-8×(-1);-8=-2×(-4);-8=-4×(-2),
则p的可能值为-1+(-8)=-9;8+1=9;-2+(-4)=-6;4+2=6.
∴整数p的所有可能值是±9,±6,
故答案为:±9,±6;
(3)∵方程分解得:(x-6)(x+2)=0,
可得x-6=0或x+2=0,
解得:x=6或x=-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=21,EC=9,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1) x2﹣5x﹣6=0;
(2) (1﹣x)2﹣1=
 ;
;(3) 8x(x+2)=3x+6;
(4)(y+
 )(y-
)(y- )=20.
)=20. -
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
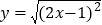 的图象与性质.小美根据学习函数的经验,对函数
的图象与性质.小美根据学习函数的经验,对函数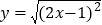 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
的图象与性质进行了探究.下面是小美的探究过程,请补充完整:(
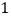 )函数
)函数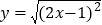 的自变量
的自变量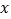 的取值范围是__________.
的取值范围是__________.(
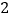 )下表是
)下表是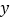 与
与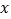 的几组对应值.
的几组对应值.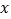

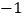
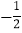
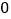

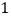

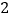

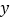

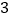
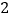
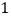
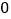
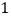
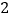
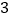

如图,在平面直角坐标系
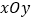 中,描出以上表中各对对应值为坐标的点.
中,描出以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象,标出函数的解析式.

(
 )结合函数的图象,写出该函数的一条性质:__________.
)结合函数的图象,写出该函数的一条性质:__________. -
科目: 来源: 题型:
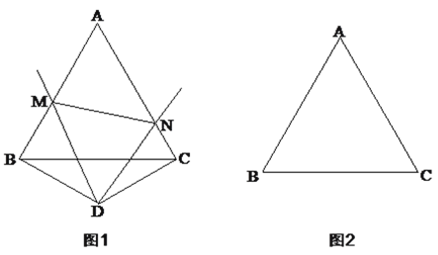
查看答案和解析>>【题目】已知:△ABC是边长为3的等边三角形,以BC为底边作一个顶角为120等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60.
(1)如图1,当点D在△ABC外部时,求证:BM+CN=MN;
(2)在(1)的条件下求△AMN的周长;
(3)当点D在△ABC内部时,其它条件不变,请在图2中补全图形,并直接写出△AMN的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形
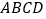 中,
中,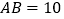 ,
,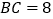 ,
,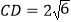 ,
,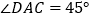 ,
,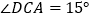 .
.(
 )求
)求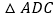 的面积.
的面积.(
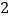 )若
)若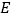 为
为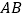 中点,求线段
中点,求线段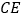 的长.
的长.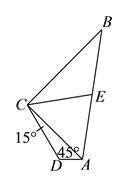
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
相关试题

