【题目】今年学校举行足球联赛,在第一阶段的比赛中,每队都进行了8场比赛,小虎足球队胜了4场,平2场,负2场,得14分;小豹足球队胜了6场,平1场,负1场,得19分.已知,记分规则中,负1场得0分.
(1)求胜1场、平1场各得多少分?
(2)足球联赛结束后,小狮足球队共参加了17场比赛,得了24分,且踢平场数是所胜场数的正整数倍,请你想一想,小狮足球队所负场数有______种可能性.
参考答案:
【答案】(1)胜1场得3分,平1场得1分;(2)2
【解析】
(1)设胜1场得x分,平1场得y分,根据题意得到二元一次方程组即可求解;
(2)设小狮足球队胜a场,平na场,负b场(a,n,b均是正整数),根据题意得到方程组,化简得到关于a,b的二元一次方程,求出其正整数解,再找到符合题意的即可求解.
解:(1)设胜1场得x分,平1场得y分
由题意得![]()
解之得![]()
答:胜1场得3分,平1场得1分
(2)设小狮足球队胜a场,平na场,负b场(a,n,b均是正整数),
根据题意得![]() ,
,
合并得2a-b=7
求得其正整数解为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
当![]() 时,平场数为12,符合题意;
时,平场数为12,符合题意;
当![]() 时,平场数为9,不符合题意;
时,平场数为9,不符合题意;
当![]() 时,平场数为6,符合题意;
时,平场数为6,符合题意;
当![]() 时,平场数为3,不符合题意;
时,平场数为3,不符合题意;
当![]() 时,平场数为0,不符合题意;
时,平场数为0,不符合题意;
故负场数有2种可能性,
故答案为:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1=
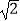 ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ 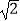 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ 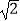 ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= . 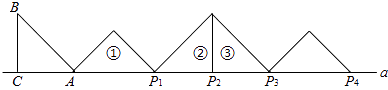
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点 D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有10名销售业务员,去年每人完成的销售额情况如表:

(1)求10名销售员销售额的平均数、中位数和众数.(单位:万元)
(2)为了调动员工积极性,公司准备采取超额有奖措施,请问把标准定为多少万元时最合适?
-
科目: 来源: 题型:
查看答案和解析>>【题目】书籍是人类进步的阶梯.联合国教科文组织把每年的4月23日确定为“世界读书日”.某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:

请你根据以上信息解答下列问题:
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有4000名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.

解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠APC与∠BAP、∠PCD之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:

(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.
相关试题

