搜索
【题目】如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1 ， 此时AP1= 
；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2 ， 此时AP2=1+ ；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3 ， 此时AP3=2+ ；…，按此规律继续旋转，直至得到点P2015为止．则AP2015= ．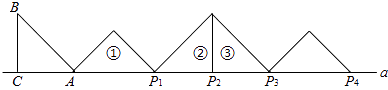 
参考答案：
【答案】1343+672 
【解析】解：AP1= 
，AP2=1+ ，AP3=2+ ；
AP4=2+2 ；AP5=3+2 ；AP6=4+2 ；
AP7=4+3 ；AP8=5+3 ；AP9=6+3 ；
∵2015=3×671+2，
∴AP2013=（2013﹣671）+671 =1342+671 ，
∴AP2014=1342+671 + =1342+672 ，
∴AP2015=1342+672 +1=1343+672 ．
所以答案是：1343+672 ．
【考点精析】解答此题的关键在于理解旋转的性质的相关知识，掌握①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．
-
科目： 来源： 题型：
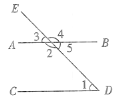
查看答案和解析>>【题目】如图,直线AB，CD被DE所截，则∠1和 是同位角，∠1和 是内错角，∠1和 是同旁内角；
(2)在(1)中，如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由：
因为∠5=∠1( )，
∠5=∠3( )，
所以∠1=∠3( ).
-
科目： 来源： 题型：
查看答案和解析>>【题目】2010年春季以来，我国西南地区遭受了严重的旱情，某校学生会自发组织了“保护水资源从我做起”的活动．同学们采取问卷调查的方式，随机调查了本校150名同学家庭月人均用水量和节水措施情况．以下是根据调查结果作出的统计图的一部分．
请根据以上信息解答问题：
(1)补全图1和图2；
(2)如果全校学生家庭总人数约为3 000人，根据这150名同学家庭月人均用水量，估计全校学生家庭月用水总量．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学为调查本校学生平均每天完成作业所用时间的情况，随机调查了50名同学，如图是根据调查所得数据绘制的统计图的一部分．
请根据以上信息，解答下列问题：
(1)将统计图补充完整；
(2)若该校共有1 800名学生，根据以上调查结果估计该校全体学生平均每天完成作业所用总时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC 中，点 D，E 分别在边 AC，AB 上，BD 与 CE 交于点 O，给出下列三个条件：①∠EBO＝∠DCO；②BE＝CD；③OB＝OC．
(1)上述三个条件中，由哪两个条件可以判定△ABC 是等腰三角形？(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形，写出证明过程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司有10名销售业务员，去年每人完成的销售额情况如表：
(1)求10名销售员销售额的平均数、中位数和众数．(单位：万元)
(2)为了调动员工积极性，公司准备采取超额有奖措施，请问把标准定为多少万元时最合适？
-
科目： 来源： 题型：
查看答案和解析>>【题目】今年学校举行足球联赛，在第一阶段的比赛中，每队都进行了8场比赛，小虎足球队胜了4场，平2场，负2场，得14分；小豹足球队胜了6场，平1场，负1场，得19分．已知，记分规则中，负1场得0分．
（1）求胜1场、平1场各得多少分？
（2）足球联赛结束后，小狮足球队共参加了17场比赛，得了24分，且踢平场数是所胜场数的正整数倍，请你想一想，小狮足球队所负场数有______种可能性．
相关试题
