【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2). 
(1)图2中的阴影部分的面积为;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是;
(3)根据(2)中的结论,若x+y=7,xy= ![]() ,则x﹣y=;
,则x﹣y=;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
参考答案:
【答案】
(1)(b﹣a)2
(2)(a+b)2﹣(a﹣b)2=4ab
(3)±2
(4)3a2+4ab+b2=(a+b)?(3a+b)
【解析】解:(1)阴影部分为边长为(b﹣a)的正方形,所以阴影部分的面积(b﹣a)2 , 故答案为:(b﹣a)2;(2)图2中,用边长为a+b的正方形的面积减去边长为b﹣a的正方形等于4个长宽分别a、b的矩形面积,
所以(a+b)2﹣(a﹣b)2=4ab,
故答案为:(a+b)2﹣(a﹣b)2=4ab; (3)∵(x+y)2﹣(x﹣y)2=4xy,
而x+y=7,xy= ![]() ,
,
∴72﹣(x﹣y)2=4× ![]() ,
,
∴(x﹣y)2=4,
∴x﹣y=±2,
故答案为:±2;(4)边长为(a+b)与(3a+b)的矩形面积为(a+b)(3a+b),它由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,
∴3a2+4ab+b2=(a+b)(3a+b),
故答案为:3a2+4ab+b2=(a+b)(3a+b).
(1)阴影部分为边长为(b﹣a)的正方形,然后根据正方形的面积公式求解;(2)在图2中,大正方形有小正方形和4个矩形组成,则(a+b)2﹣(a﹣b)2=4ab; (3)由(2)的结论得到(x+y)2﹣(x﹣y)2=4xy,再把x+y=7,xy= ![]() 得到(x﹣y)2=4,然后利用平方根的定义求解;(4)观察图形得到边长为(a+b)与(3a+b)的矩形由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,则有3a2+4ab+b2=(a+b)(3a+b).
得到(x﹣y)2=4,然后利用平方根的定义求解;(4)观察图形得到边长为(a+b)与(3a+b)的矩形由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,则有3a2+4ab+b2=(a+b)(3a+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC , ∠ABC=2∠C , 以B为圆心任意长为半径作弧,交BA、BC于点E、F , 分别以E、F为圆心,以大于
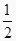 EF的长为半径作弧,两弧交于点P , 作射线BP交AC于点,则下列说法不正确的是( )
EF的长为半径作弧,两弧交于点P , 作射线BP交AC于点,则下列说法不正确的是( ) 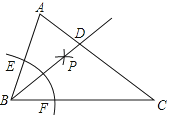
A.∠ADB=∠ABC
B.AB=BD
C.AC=AD+BD
D.∠ABD=∠BCD -
科目: 来源: 题型:
查看答案和解析>>【题目】点M(-2,1)关于x轴的对称点N的坐标是( )
A.(2,1)
B.(-2,1)
C.(-2,-1)
D.(2,-1) -
科目: 来源: 题型:
查看答案和解析>>【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中画出钝角△ABC,使它的面积为6(画一个即可);
(2)在图2中画出△DEF,使它的三边长分别为
 、
、 、5(画一个即可).并且直接写出此时三角形DEF的面积.
、5(画一个即可).并且直接写出此时三角形DEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x<y,且(a-3)x>(a-3)y,则a的取值范围是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论中正确的是( )

A.AB﹣AD>CB﹣CD
B.AB﹣AD=CB﹣CD
C.AB﹣AD<CB﹣CD
D.AB﹣AD与CB﹣CD的大小关系不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+mx+16是一个完全平方式,则m的取值是( )
A. 8 B. ﹣8 C. ±8 D. ±4
相关试题

