【题目】如图,已知等腰△ABC,AC=BC=10.AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
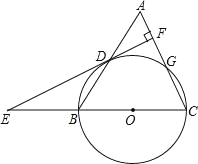
(1)求证:直线EF是⊙O的切线;
(2)求DF的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)求证直线EF是⊙O的切线,只要连接OD证明OD⊥EF即可;
(2)由BC是⊙O直径,得到CD⊥AB,在Rt△ACD中,由勾股定理得:CD=![]() =8,由于EF⊥AC,CD⊥AB,得出∠AFD=∠CDB=90°,推出△ADF∽△BCD,得到比例式,即可得到结论.
=8,由于EF⊥AC,CD⊥AB,得出∠AFD=∠CDB=90°,推出△ADF∽△BCD,得到比例式,即可得到结论.
试题解析:(1)连接CD,OD,
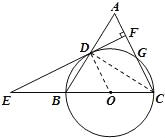
∵AC=BC,
∴∠A=∠ABC,
∵OD=OB,
∴∠ABC=∠BDO,
∴∠A=∠BDO,
∴OD∥AC,
∵EF⊥AC,
∴EF⊥OD,
∵OD为半径,
∴EF是⊙O的切线;
(2)∵BC是⊙O直径,
∴CD⊥AB,
∵AC=BC=10,又AB=12,
∴AD=BD=6,
在Rt△ACD中,由勾股定理得:CD=![]() =8,
=8,
∵EF⊥AC,CD⊥AB,
∴∠AFD=∠CDB=90°,
又∵∠A=∠CBD,
∴△ADF∽△BCD,
∴![]() ,
,
∴![]() ,即DF=
,即DF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数
 (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(1)求反比例函数
 的解析式;
的解析式;(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数
 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出
 的x的取值范围;
的x的取值范围;(3)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D,点E为y轴上一动点,CE的垂直平分线交抛物线于P,Q两点(点P在第三象限)

(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)当△CDE是直角三角形,且∠CDE=90° 时,求出点P的坐标;
(3)当△PBC的面积为
 时,求点E的坐标.
时,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴上,直线y=3x-4经过等腰Rt△AOB的直角顶点A,交y轴于C点,双曲线y=
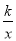 也经过A点.
也经过A点.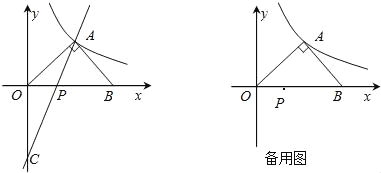
(1)求点A的坐标和k的值;
(2)若点P为x轴上一动点.在双曲线上是否存在一点Q,使得△PAQ是以点A为直角顶点的等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①所有的有理数都能用数轴上的点表示;
②符号不同的两个数互为相反数;
③有理数分为正数和负数;
④两数相减,差一定小于被减数;
⑤两数相加,和一定大于任何一个加数.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的各组线段中,不能组成三角形的是( )
A.1.5,2.5,3.5
B.2,3,5
C.6,8,10
D.4,3,3
相关试题

