搜索
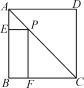
【题目】如图，P为正方形ABCD的对角线AC上任意一点，PE⊥AB于E，PF⊥BC于F，若AC＝
，则四边形PEBF的周长为( )
A. B. 2 C. 2 D. 1
参考答案：
【答案】C
【解析】
由题中条件可得四边形FBFP为矩形，又点P在对角线上，可得PE=AE，进而可求其周长等于正方形的边长的2倍，根据勾股定理，可得四边形的边长为1，所以四边形PEBF的周长为2.
由题意可得，四边形EBFP为矩形，所以BF=PE，PF=BE，又点P在对角线AC上，∠BAC=45°，所以AE=PE，所以四边形PEBF的周长为BE+EP+PF+BF=BE+AE+PF+AE=2AB.
∵AC=
，AB=BC，
∴2AB2=AC2，即2AB2=2，
∴AB=1，
∴四边形PEBF的周长为2AB=2.
故选C.
-
科目： 来源： 题型：
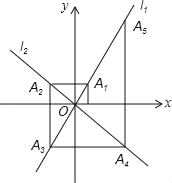
查看答案和解析>>【题目】如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l1，l2，过点（1，0）作x轴的垂线交l1于点A1…过点A1作y轴的垂线交L2于点A2，过点A2作x轴的垂线交于点A3，过点A3作y轴的垂线交L2于点A4，依次进行下去，则点A2018的坐标为（ ）
A. （﹣21009，21009） B. （﹣21009，﹣21010）
C. （﹣1009，1009） D. （﹣1009，﹣2018）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（ ）.
A. OA＝OC，OB＝OD B. ∠BAD＝∠BCD，AB∥CD
C. AD∥BC，AD＝BC D. AB＝CD，AO＝CO
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）
A. △AFD≌△DCE B. AF=
AD C. AB=AF D. BE=AD﹣DF -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，分别以线段AC的两个端点A，C为圆心，大于
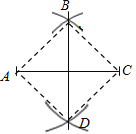
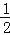AC的长为半径画弧，两弧相交于B，D两点，连接BD，AB，BC，CD，DA，以下结论：①BD垂直平分AC；
②AC平分∠BAD；
③AC=BD；
④四边形ABCD是中心对称图形．
其中正确的有（ ）
A. ①②③ B. ①③④ C. ①②④ D. ②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，曲线AB是顶点为B，与y轴交于点A的抛物线y=﹣x2+4x+2的一部分，曲线BC是双曲线y=
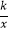的一部分，由点C开始不断重复“A﹣B﹣C”的过程，形成一组波浪线，点P（2017，m）与Q（2025，n）均在该波浪线上，过点P、Q分别作x轴的垂线，垂足为M、N，连结PQ，则四边形PMNQ的面积为（ ）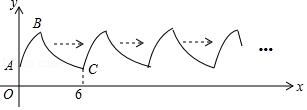 
A.72
B.36
C.16
D.9 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点，若AC⊥BD，且AC≠BD，则四边形EFGH的形状是 .（填“梯形”、“矩形”或“菱形”）
相关试题
