【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y= ![]() 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( ) 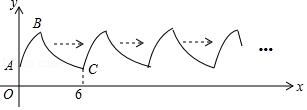
A.72
B.36
C.16
D.9
参考答案:
【答案】B
【解析】解:如图所示,A,C之间的距离为6, 2017÷6=336…1,故点P离x轴的距离与点P'离x轴的距离相同,
在y=﹣x2+4x+2中,当x=1时,y=5,即点P'离x轴的距离为5,
∴P'M'=5,
2025﹣2017=8,故点Q与点P的水平距离为8,
即M'N'=MN=8,点Q离x轴的距离与点Q'离x轴的距离相同,
由题可得,抛物线的顶点B的坐标为(2,6),故A,B之间的水平距离为6,且k=12,
∵点D与点Q'的水平距离为1+8﹣6﹣2=1,点C与点Q'的水平距离为1+2=3,
∴在y= ![]() 中,当x=3时,y=4,即点Q'离x轴的距离为4,
中,当x=3时,y=4,即点Q'离x轴的距离为4,
∴Q'N'=4,
∵四边形P'M'N'Q'的面积为 ![]() =36,
=36,
∴四边形PMNQ的面积为36,
故选:B.
【考点精析】根据题目的已知条件,利用比例系数k的几何意义和二次函数的性质的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=
 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=
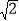 ,则四边形PEBF的周长为( )
,则四边形PEBF的周长为( )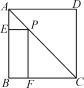
A.
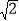 B. 2
B. 2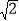 C. 2 D. 1
C. 2 D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以线段AC的两个端点A,C为圆心,大于
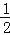 AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:
AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:①BD垂直平分AC;
②AC平分∠BAD;
③AC=BD;
④四边形ABCD是中心对称图形.
其中正确的有( )
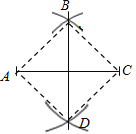
A. ①②③ B. ①③④ C. ①②④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,若AC⊥BD,且AC≠BD,则四边形EFGH的形状是 .(填“梯形”、“矩形”或“菱形”)
-
科目: 来源: 题型:
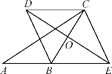
查看答案和解析>>【题目】已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
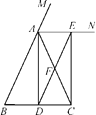
(1)求证:四边形ADCE为矩形;
(2)连接DE,交AC于点F,请判断四边形ABDE的形状,并证明;
(3)线段DF与AB有怎样的关系?请直接写出你的结论.
相关试题

