搜索
【题目】下列说法中：
①在Rt△ABC中，∠C=90°，CD为AB边上的中线，若CD=2，则AB=4；
②八边形的内角和度数为1080°；
③2、3、4、3这组数据的方差为0.5；
④分式方程
=
的解为x=
；
⑤已知菱形的一个内角为60°，一条对角线为2，则另一对角线为2
．
正确的序号有（ ）
A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤
参考答案：
【答案】B
【解析】分析：根据直角三角形斜边上的中线等于斜边的一半可判断出①的正误；根据多边形的内角和公式：
（
且
为整数）可以计算出②的正误；根据方差公式可计算出③的正误；解分式方程可判断出④的正误；⑤要分两种情况进行讨论．
详解：①根据直角三角形斜边上的中线等于斜边的一半可得AB=2CD=4，故此说法正确；
②八边形的内角和度数为：
故此说法正确；
③2、3、4、3这组数据的平均数为(2+3+4+3)÷4=3，
方差为
故此说法正确；
④分式方程
的解为
，说法正确；
⑤已知菱形的一个内角为
,一条对角线为2，则另一对角线为
或
，故此说法错误；
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，数轴上有两点A、B对应的数分别为1，5，点P为数轴上一动点，其对应的数为x．
（1）若点P到点A、B的距离相等，求点A、B的距离及x的值．
（2）数轴上是否存在点P，使得点P到点A、B的距离之和最小？若存在，请求出最小值；并求出取得最小值时x可以取的整数值；若不存在，说明理由．
（3）点A、B分别以3个单位长度/秒，2个单位长度/秒的速度向右运动，同时点P以4个单位长度/秒的速度从O点向左运动，当遇到A时，点P立即以不变的速度向右运动，当遇到B时，点P立即以不变的速度向左运动，并不停往返于点A与点B之间，求当点A与点B重合时，点P所经过的总路程是多少？
-
科目： 来源： 题型：
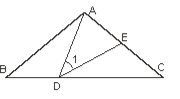
查看答案和解析>>【题目】如图,⊿ABC中,AB=AC,∠BAC=
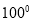,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.(1)若∠BAD=
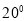,求∠EDC的度数;(2)当DC=AC时,求证:⊿ABD≌⊿DCE ;
(3)当∠BAD的度数是多少时,⊿ADE能成为等腰三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点
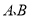都在数轴上，
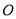为原点．（1）点
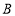表示的数是 ；（2）若点
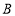以每秒3个单位长度的速度沿数轴运动，则1秒后点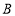表示的数是 ；（3）若点
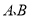都以每秒3个单位长度的速度沿数轴向右运动，而点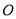不动，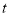
秒后有一个点是一条线段的中点，求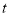的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小刚和小强从
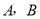两地同时出发，小刚骑自行车，小强步行，沿同一条路线相向匀速而行．出发后两小时两人相遇，相遇时小刚比小强多行进24千米．相遇后0．5小时小刚到达
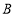地．（1）两人的行进速度分别是多少？
（2）相遇后经过多少时间小强到达
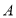地？（3）
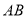两地相距多少千米？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=x2-2x-3，点P在该函数的图象上，点P到x轴、y轴的距离分别为d1、d2．设d=d1+d2,下列结论中： ①d没有最大值； ②d没有最小值； ③ -1＜x＜3时,d 随x的增大而增大； ④满足d=5的点P有四个.其中正确结论的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某港口在某天从0时到12时的水位情况变化曲线．
（1）在这一问题中，自变量是什么？
（2）大约在什么时间水位最深，最深是多少？
（3）大约在什么时间段水位是随着时间推移不断上涨的？
相关试题
