【题目】已知,数轴上有两点A、B对应的数分别为1,5,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、B的距离相等,求点A、B的距离及x的值.
(2)数轴上是否存在点P,使得点P到点A、B的距离之和最小?若存在,请求出最小值;并求出取得最小值时x可以取的整数值;若不存在,说明理由.
(3)点A、B分别以3个单位长度/秒,2个单位长度/秒的速度向右运动,同时点P以4个单位长度/秒的速度从O点向左运动,当遇到A时,点P立即以不变的速度向右运动,当遇到B时,点P立即以不变的速度向左运动,并不停往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
参考答案:
【答案】(1)1,5,2;(2)存在,最小值为6,x可以取的整数值有1、0、1、2、3、4、5;(3)48
【解析】
(1)根据数轴上的两点距离公式和中点公式列式求解即可;
(2)分类讨论点P分别在点A左侧、点A、点B之间、点B右侧时分别求出,进行比较即可求出最小值;
(3)设经过t分钟点A与点B重合,根据点A比点B运动的距离多6,列出方程,求出t的值,即为点P的运动时间,再乘以点P运动的速度,即可得点P所经过的总路程.
解:(1)∵点A、B对应的数分别为1,5,
∴![]() ,即点A、B的距离为6;
,即点A、B的距离为6;
∵点P到点A、B的距离相等,则P为AB中点,
则有:![]() ,所以
,所以![]() ;
;
(2)数轴上存在点P,使得点P到点A、B的距离之和最小,
当点P在点A左侧时,点P到点A、B的距离之和为:PA+PB=2PA+AB=2PA+6,
当点P在点A、点B之间时,点P到点A、B的距离之和为:PA+PB=AB=6,
当点P在点B右侧时,点P到点A、B的距离之和为:PA+PB=2PB+AB=2PA+6,
所以当点P在点A、点B之间时(含点A、点B),点P到点A、B的距离之和最小,最小值为6,
点A、点B之间的整数值有1、0、1、2、3、4、5,即为x可以取的整数值;
(3)设经过t分钟点A与点B重合,依题意得:
1+3t=5+2t+6,解得:t=12,
所以4t=4×12=48,
所以点P所经过的总路程是48个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用小立方块搭一几何体,它的主视图和俯视图如图所示,这个几何体最少要a个立方块,最多要b个立方块.

(1)求a,b的值
(2)若有理数x,y满足
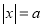 ,
, ,且xy<0,求x+y的值.
,且xy<0,求x+y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
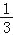 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
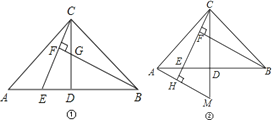
查看答案和解析>>【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点 H,交CD的延长线于点M(如图②),
求证:CM=BE.
-
科目: 来源: 题型:
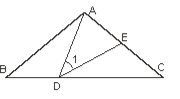
查看答案和解析>>【题目】如图,⊿ABC中,AB=AC,∠BAC=
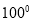 ,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.(1)若∠BAD=
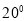 ,求∠EDC的度数;
,求∠EDC的度数;(2)当DC=AC时,求证:⊿ABD≌⊿DCE ;
(3)当∠BAD的度数是多少时,⊿ADE能成为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
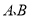 都在数轴上,
都在数轴上,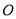 为原点.
为原点.(1)点
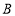 表示的数是 ;
表示的数是 ;(2)若点
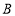 以每秒3个单位长度的速度沿数轴运动,则1秒后点
以每秒3个单位长度的速度沿数轴运动,则1秒后点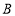 表示的数是 ;
表示的数是 ;(3)若点
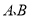 都以每秒3个单位长度的速度沿数轴向右运动,而点
都以每秒3个单位长度的速度沿数轴向右运动,而点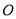 不动,
不动,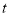 秒后有一个点是一条线段的中点,求
秒后有一个点是一条线段的中点,求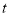 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:
①在Rt△ABC中,∠C=90°,CD为AB边上的中线,若CD=2,则AB=4;
②八边形的内角和度数为1080°;
③2、3、4、3这组数据的方差为0.5;
④分式方程
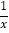 =
=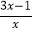 的解为x=
的解为x= ;
;⑤已知菱形的一个内角为60°,一条对角线为2,则另一对角线为2
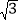 .
.正确的序号有( )
A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤
相关试题

