搜索
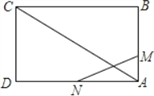
【题目】如图，已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：
（1）经过多少时间，△AMN的面积等于矩形ABCD面积的九分之一？
（2）是否存在时刻t，使以A,M,N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．
参考答案：
【答案】（1）1秒或2秒；（2）
秒或
秒
【解析】试题分析：（1）设时间为x，根据速度表示出所涉及到的线段的长度，根据△AMN的面积等于矩形ABCD面积的
，列方程求解即可；（2）先假设相似，利用相似中的比例线段列出方程，有解的且符合题意的t值即可说明存在，反之则不存在．
试题解析：
（1）设经过x秒，△AMN的面积等于矩形ABCD面积的
，
由题意得DN=2x，AN=6-2x，AM=x，
∵矩形ABCD中AB=3，BC=6，
∴AD=BC=6，CD=AB=3，
矩形ABCD的面积为：ABAD=3×6=18，
△AMN的面积=
ANAM＝
x(62x)＝3xx2=
×18，
可得方程x2-3x+2=0，
解得x1=1，x2=2，
答：经过1秒或2秒，△AMN的面积等于矩形ABCD面积的
；
（2）由题意得DN=2t，AN=6-2t，AM=t，
若△NMA∽△ACD，
则有
，即
，
解得x=1.5，
若△MNA∽△ACD
则有
，即
，
解得x=2.4，
答：当t=1.5秒或2.4秒时，以A、M、N为顶点的三角形与△ACD相似．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1) 知识储备
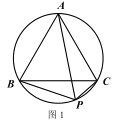
①如图 1，已知点 P 为等边△ABC 外接圆的弧BC 上任意一点．求证：PB+PC= PA.
②定义：在△ABC 所在平面上存在一点 P，使它到三角形三顶点的距离之和最小，则称点 P 为△ABC
的费马点，此时 PA+PB+PC 的值为△ABC 的费马距离．
(2)知识迁移
①我们有如下探寻△ABC (其中∠A，∠B，∠C 均小于 120°)的费马点和费马距离的方法：
如图 2，在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆，根据(1)的结论，易知线段____的长度即为△ABC 的费马距离.
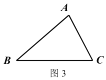
②在图 3 中，用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题（正确的打√，错误的打×）：
ⅰ.任意三角形的费马点有且只有一个（__________）；
ⅱ.任意三角形的费马点一定在三角形的内部（__________）.
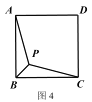
②已知正方形 ABCD，P 是正方形内部一点，且 PA+PB+PC 的最小值为
，求正方形 ABCD 的边长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况，随机抽取部分学生做了一次问卷调查，要求学生选出自己喜欢的一个版面，将调查数据进行了整理、绘制成部分统计图如下：
请根据图中信息，解答下列问题：
（1）第一版=____%，“第四版”对应扇形的圆心角为________°；
（2）请你补全条形统计图；
（3）若该校有1200名学生，请你估计全校学生中最喜欢“第三版”的人数．
-
科目： 来源： 题型：
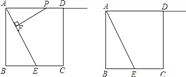
查看答案和解析>>【题目】如图，正方形 ABCD 的边长为 4，E 是 BC 的中点，点 P 在射线 AD 上，过点 P 作 PF⊥AE，垂足为 F．
（1）求证：△PFA∽△ABE；
（2）当点 P 在射线 AD 上运动时，设 PA=x，是否存在实数 x，使以 P，F，E 为顶点的三角形也与△ABE
相似？若存在，求出 x 的值；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】按下列程序进行运算（如图）
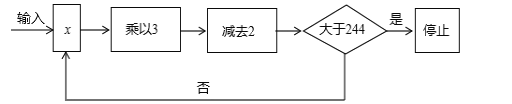
规定：程序运行到“判断结果是否大于244”为一次运算，若运算进行了5次才停止，则x的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，AF=BE，AE与DF相交于点O．
（1）求证：△DAF≌△ABE；
（2）写出线段AE、DF的数量和位置关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，动点A从原点出发向数轴负方向运动，同时，动点B也从原点出发向数轴正方向运动，3秒后两点相距15个单位长度，已知动点A、B的速度比是1：4（速度单位：1单位长度/秒）。
（1）求两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置；
（2）若A、B两点分别从（1）中标出的位置同时向数轴负方向运动，问经过几秒，原点恰好处在两个动点的正中间？
相关试题
