【题目】如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.

(1)求证:△DAF≌△ABE;
(2)写出线段AE、DF的数量和位置关系,并说明理由.
参考答案:
【答案】(1)详见解析;(2)AE=DF,AE⊥D
【解析】
(1)根据正方形得性质很容易得到,DA=AB,∠DAF=∠ABE=90°,再根据AF=BE,即可证明△DAF≌△ABE.
(2)根据第一问得到的全等,可以很容易得到AE与DF的数量关系,而要根据图形可以猜测其位置关系为垂直,因此只需要证明到∠AOD=90°即可,因此可以转化到算∠ADO+∠DAO的度数.
(1)∵四边形ABCD是正方形,
∴DA=AB,∠DAF=∠ABE=90°,
∵AF=BE,
∴△DAF≌△ABE(SAS);
(2)AE=DF,AE⊥DF,理由如下:
由(1)得:△DAF≌△ABE,
∴DF=AE,∠ADF=∠BEA,
∵∠DAO+∠EAB=∠DAF=90°,
∴∠DAO+∠ADF=90°,
∴∠DAO=90°,
∴AE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图
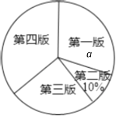
各版面选择人数的条形统计图
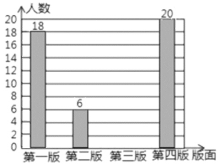
请根据图中信息,解答下列问题:
(1)a=______%,“第四版”对应扇形的圆心角为 °;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2
(1)求实数k的取值范围。
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明.
如图、
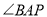 与
与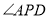 互补,
互补,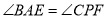 ,求证:
,求证: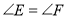 .对于本题小丽是这样证明的,请你将她的证明过程补充完整.
.对于本题小丽是这样证明的,请你将她的证明过程补充完整.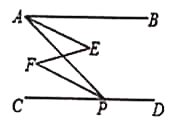
证明:
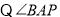 与
与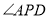 互补,(已知)
互补,(已知)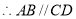 .(________________________________)
.(________________________________)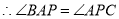 .(________________________________)
.(________________________________)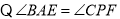 ,(已知)
,(已知)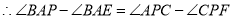 ,(等量代换)
,(等量代换)即_______________=_______________.
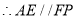 .(________________________________)
.(________________________________)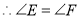 .(________________________________)
.(________________________________) -
科目: 来源: 题型:
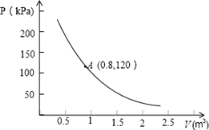
查看答案和解析>>【题目】某气球内充满了一定量的气体,当温度不变时,气球内气体的压强P(kPa)是气体体积V(m3)的反比例函数,其图像如图所示.
(1)求这一函数的表达式;
(2)当气体压强为48kPa时,求V的值?
(3)当气球内的体积小于0.6m3时,气球将爆炸,为了安全起见,气体的压强不大于多少?
-
科目: 来源: 题型:
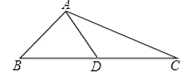
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=13,边BC上的中线AD=6.
(1)以点D为对称中心,作出△ABD的中心对称图形;
(2)求点A到BC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)按要求将下列几何体进行分类,并将分类后几何体的名称写在对应的括号内.

柱体:{ …}
锥体:{ …}
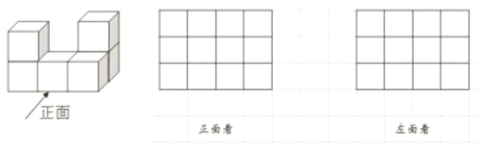
(2)6个完全相同的正方体组成如图所示的几何体,画出该几何体从正面,左面看到的形状图(用阴影画在所给的方格中)
相关试题

