【题目】(1) 知识储备
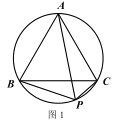
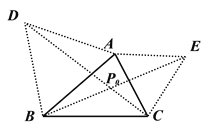
①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.
②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC
的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
(2)知识迁移
①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
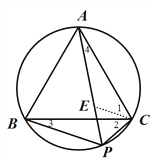
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段____的长度即为△ABC 的费马距离.
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个(__________);
ⅱ.任意三角形的费马点一定在三角形的内部(__________).
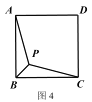
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为![]() ,求正方形 ABCD 的
,求正方形 ABCD 的
边长.

参考答案:
【答案】 AD √ ×
【解析】分析:(1)根据已知首先能得到△PCE为等边三角形,进而得出△ACE≌△BPC,即可得证;
(2)①仔细阅读新知的概念,结合图形特点,直接有结论判断即可;
②根据尺规作图,作等边三角形即可求得费马点;
(3)①ⅰ.根据作图可知费马点有且只有一个,ⅱ.由图1和图2,可知任意三角形的费马点不一定都在三角形的内部;
②将△ABP沿点B逆时针旋转60°到△A1BP1,过A1作A1H⊥BC,交CB的延长线于H,连接P1P,根据等边三角形的判定与性质,得到△P1PB是正三角形,进而得出∠A1BH=30°,然后由正方形的性质和30°角直角三角形的性质,根据勾股定理求出正方形的边长.
详解:(1)①证明:在PA上取一点E,使PE=PC,连接CE,
∵正三角形ABC
∴∠APC=∠ABC=60°
又∵PE=PC,∴△PEC是正三角形
∴CE=CP ∠ACB=∠ECP=60°
∴∠1=∠2
又∵∠3=∠4 BC=AC
∴△ACE≌△BCP (ASA)
∴AE=BP
即:BP+CP=AP.
(2)①线段 AD 的长度即为△ABC的费马距离.
②过AB和AC分别向外作等边三角形,连接CD,BE,
交点即为P0.
(3)①ⅰ.( √ ) ②ⅱ.( × )
②解:将△ABP沿点B逆时针旋转60°到△A1BP1,
过A1作A1H⊥BC,交CB的延长线于H,连接P1P,
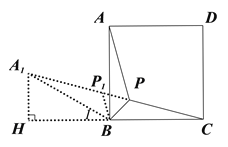
易得:A1B=AB,PB=P1B,PA=P1 A1,∠P1BP=∠A1BA=60°
∵PB=P1B ∠P1BP=60°
∴△P1PB是正三角形
∴PP1=PB
∵PA+PB+PC的最小值为![]()
∴P1A1+PP1+PC的最小值为![]()
∴A1,P1,P,C在同一直线上,即A1C=![]()
设正方形的边长为2x
∵∠A1BA=60° ∠CBA=90°
∴∠1=30°
在Rt△A1HB中,A1B=AB=2x,∠1=30°
得:A1H=x,BH=![]()
在Rt△A1HC中,由勾股定理得:![]()
解得:x1=1 x2=1(舍去)
∴正方形ABCD的边长为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小高从家门口骑车去离家4千米的单位上班,先花3分钟走平路1千米,再走上坡路以0.2千米/分钟的速度走了5分钟,最后走下坡路花了4分钟到达工作单位,若设他从家开始去单位的时间为t(分钟),离家的路程为y(千米),则y与t(8<t≤12)的函数关系为( )
A. y=0.5t(8<t≤12) B. y=0.5t+2(8<t≤12)
C. y=0.5t+8(8<t≤12) D. y="0." 5t-2(8<t≤12)
-
科目: 来源: 题型:
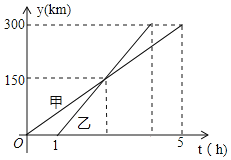
查看答案和解析>>【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.
(1)求乙车离开A城的距离y关于t的函数解析式;
(2)求乙车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当前,交通拥堵是城市管理的一大难题.我市城东高架桥的开通为分流过境车辆、缓解市内交通压力 起到了关键作用,但为了保证安全,高架桥上最高限速 80 千米/小时.在一般条件下,高架桥上的车流 速度 v(单位:千米/小时)是车流密度 x(单位:辆/千米)的函数,当桥上的车流密度达到 180 辆/千 米时,造成堵塞,此时车流速度为 0;当 0≤x≤20 时,桥上畅通无阻,车流速度都为 80 千米/小时, 研究表明:当 20≤x≤180 时,车流速度 v 是车流密度 x 的一次函数.
(1)当 0≤x≤20 和 20≤x≤180 时,分别写出函数 v 关于 x 的函数关系式;
(2)当车流密度 x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)w=x·v可以达到最大,并求出最大值;
(3)某天早高峰(7:30—9:30)经交警部门控制管理,桥上的车流速度始终保持 40 千米/小时,问这天 早高峰期间高架桥分流了多少辆车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)第一版=____%,“第四版”对应扇形的圆心角为________°;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
-
科目: 来源: 题型:
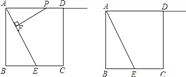
查看答案和解析>>【题目】如图,正方形 ABCD 的边长为 4,E 是 BC 的中点,点 P 在射线 AD 上,过点 P 作 PF⊥AE,垂足为 F.
(1)求证:△PFA∽△ABE;
(2)当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶点的三角形也与△ABE
相似?若存在,求出 x 的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的九分之一?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
相关试题

