【题目】如图,在平面直角坐标系中,直线l:y= ![]() x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此作法进行下去,则OA2017= .
x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此作法进行下去,则OA2017= . 
参考答案:
【答案】22016
【解析】解:直线y= ![]() x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1 , 可知B1点的坐标为(
x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1 , 可知B1点的坐标为( ![]() ,1),
,1),
以原点O为圆心,OB1长为半径画弧交y一轴于点A2 , OA2=OB1=2OA1=2,点A2的坐标为(0,2),
这种方法可求得B2的坐标为(2 ![]() ,2),
,2),
故点A3的坐标为(0,4),B3的坐标为(4 ![]() ,4),
,4),
点A4的坐标为(0,8),B4的坐标为(8 ![]() ,8),
,8),
此类推便可求出点An的坐标为(0,2n﹣1).
所以点A2017的坐标为(0,22016).
所以OA2017=22016 .
所以答案是:22016 .
【考点精析】本题主要考查了数与式的规律的相关知识点,需要掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B,C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.

初步感知:
(1)如图1,当点D在边BC上时,①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
(3)如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把
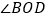 分成两部分;
分成两部分;(1)直接写出图中
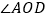 的对顶角为 ,
的对顶角为 ,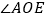 的邻补角为 ;
的邻补角为 ;(2)若
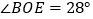 ,且
,且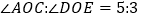 ,求
,求 的度数.
的度数.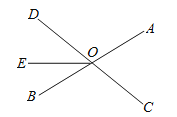
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(﹣3,0).

(1)求该抛物线的解析式;
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;
(3)在第一象限内的该抛物线上是否存在点G,使△AGC的面积与(2)中△APE的最大面积相等?若存在,请求出点G的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
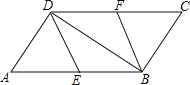
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF ;
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为
 .
. 
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

相关试题

