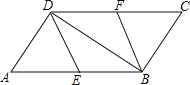
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

参考答案:
【答案】(1)证明见解析(2)当∠BAC=90°时,矩形AEBD是正方形
【解析】试题分析:(1)利用平行四边形的判定首先得出四边形AEBD是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;
(2)利用等腰直角三角形的性质得出AD=BD=CD,进而利用正方形的判定得出即可.
(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
 x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此作法进行下去,则OA2017= .
x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此作法进行下去,则OA2017= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF ;
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为
 .
. 
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织班团活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品,已知笔记本2元/本,中性笔1元/支,且每种奖品至少买1件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
(3)从上述方案中任选一种方案购买,求买到的中性笔与笔记本数量相等的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.

(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ,求
,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】当前正值草莓销售季节,小李用2000元在安塞区草莓基地购进草莓若干进行销售,由于销售状况良好,他又拿出6000元资金购进该种草莓,但这次的进货价比第一次的进货价提高了20%,购进草莓数量比第一次的2倍还多20千克。求该种草莓第一次进价是每千克多少元?
相关试题

