搜索
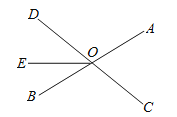
【题目】如图，直线AB、CD相交于点O，OE把
分成两部分；
（1）直接写出图中
的对顶角为 ，
的邻补角为 ；
（2）若
，且
，求
的度数.
参考答案：
【答案】（1）∠BOC，∠BOE;(2)138°
【解析】分析：（1）利用对顶角、邻补角的定义直接回答即可；
（2）根据对顶角相等和∠AOC：∠DOE=5：3，得到∠BOD：∠DOE=5：3，设∠BOD=5x，则∠DOE=3x，∠BOE=2x．求出x的值，即可得到结论．
详解：（1）∠AOD的对顶角为∠BOC，∠AOE的邻补角为∠BOE；
（2）∵∠AOC=∠BOD，∠AOC：∠DOE=5：3，∴∠BOD：∠DOE=5：3．
设∠BOD=5x，则∠DOE=3x，∴∠BOE=∠BOD-∠DOE=5x-3x=2x ．
∵∠BOE=28°，∴2x=28°， ∴x=14°，
∴∠DOE=3x=3×14°=42°．
∵∠DOE+∠COE=180°，
∴∠COE=180°-∠DOE=180°-42°=138°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，点E、F在对角线BD上，且BF＝DE．
⑴求证：四边形AECF是菱形．
⑵若AB＝2，BF＝1，求四边形AECF的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据提示填空（8分）
如图，EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
因为EF∥AD
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°(_____________________)
因为∠BAC=80° 所以∠AGD=_______
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，△ABC为等边三角形，点D为直线BC上一动点（点D不与B，C重合）．以AD为边作菱形ADEF，使∠DAF=60°，连接CF．
初步感知：
（1）如图1，当点D在边BC上时，①求证：∠ADB=∠AFC；②请直接判断结论∠AFC=∠ACB+∠DAC是否成立；
（2）如图2，当点D在边BC的延长线上时，其他条件不变，结论∠AFC=∠ACB+∠DAC是否成立？请写出∠AFC、∠ACB、∠DAC之间存在的数量关系，并写出证明过程；
（3）如图3，当点D在边CB的延长线上时，且点A、F分别在直线BC的异侧，其他条件不变，请补全图形，并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系． -
科目： 来源： 题型：
查看答案和解析>>【题目】将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中，点O为坐标原点，点C、A分别在x、y轴的正半轴上，一条抛物线经过点A、C及点B（﹣3，0）．
（1）求该抛物线的解析式；
（2）若点P是线段BC上一动点，过点P作AB的平行线交AC于点E，连接AP，当△APE的面积最大时，求点P的坐标；
（3）在第一象限内的该抛物线上是否存在点G，使△AGC的面积与（2）中△APE的最大面积相等？若存在，请求出点G的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线l：y=
x，点A1（0，1），过点A1作y轴的垂线交直线l于点B1 ， 以原点O为圆心，OB1长为半径画弧交y轴于点A2；再过点A2作y轴的垂线交直线l于点B2 ， 以原点O为圆心，OB2长为半径画弧交y轴于点A3 ， …，按此作法进行下去，则OA2017= ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，连接DE、BF、BD．
（1）求证：△ADE≌△CBF ；
（2）当AD⊥BD时，请你判断四边形BFDE的形状，并说明理由.
相关试题
