搜索
【题目】方程3x+1=7的根是 ．
参考答案：
【答案】x=2
【解析】解：移项得，3x=7﹣1， 合并同类项得，3x=6，
系数化为1得，x=2．
所以答案是：x=2．
【考点精析】根据题目的已知条件，利用解一元一次方程的步骤的相关知识可以得到问题的答案，需要掌握先去分母再括号，移项变号要记牢．同类各项去合并，系数化“1”还没好．求得未知须检验，回代值等才算了．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）化简：5m2－7n－8mn＋5n－9m2＋8mn．
（2）已知：a－2b＝4，ab＝1．试求代数式(－a＋3b＋5ab)－(5b－2a＋6ab)的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程ax2+bx﹣2015=0有一个根为x=1，写出一组满足条件的实数a，b的值：a= ，b=
-
科目： 来源： 题型：
查看答案和解析>>【题目】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪灵感.他惊喜地发现：当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1摆放，其中∠DAB=90°，求证：a2+b2=c2.
证明：连接DB，过点D作BC边上的高DF，则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=
b2+ab.又∵S四边形ADCB=S△ADB+S△DCB=
c2+a(b－a)，∴
b2+ab=c2+a(b－a)，∴a2+b2=c2.
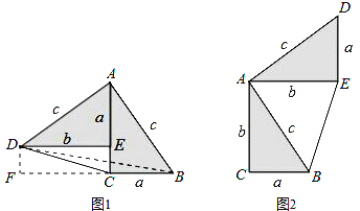
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°.
求证：a2+b2=c2.
证明：连接 ，
∵S五边形ACBED= ，
又∵S五边形ACBED= ，
∴ ，
∴a2+b2=c2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列语句中，是命题的为（ ）
A.在线段AB上任取一点CB.对顶角相等
C.过点O作直线a∥bD.锐角都相等吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一条直线上有A，B，C三点，AB=6cm，BC=2cm，点P，Q分别是线段AB，BC的中点，则PQ= ______ cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元.
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元.
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
（3）实际进货时，厂家对A型电脑出厂价下调m(0<m<100)元，且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变，请你根据以上信息及(2)中条件，设计出使这100台电脑销售总利润最大的进货方案.
相关试题
