Question

【题目】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪灵感.他惊喜地发现：当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程：

将两个全等的直角三角形按图1摆放，其中∠DAB=90°，求证：a2+b2=c2.

证明：连接DB，过点D作BC边上的高DF，则DF=EC=b-a.

∵S四边形ADCB=S△ACD+S△ABC=b2+ab.

又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b－a)，

∴b2+ab=c2+a(b－a)，

∴a2+b2=c2.

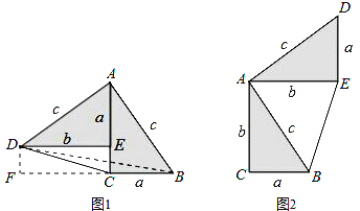
请参照上述证法，利用图2完成下面的证明：

将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°.

求证：a2+b2=c2.

证明：连接 ，

∵S五边形ACBED= ，

又∵S五边形ACBED= ，

∴ ，

∴a2+b2=c2.

Answer 1

【答案】见解析.

【解析】试题分析：首先连结BD，过点B作DE边上的高BF，则BF=b-a，表示出S五边形ACBED，进而得出答案.

试题解析：如图2，连接BD，过点B作DE边上的高BF，则BF=b-a，

∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab，

又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a)，

∴ab+b2+ab=ab+c2+a(b-a)，

∴a2+b2=c2.