【题目】如图是一座人行天桥的示意图，天桥的高度是10米，CB⊥DB ， 坡面AC的倾斜角为45° ． 为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC的坡度为i= ：3 ． 若新坡角下需留3米宽的人行道，问离原坡角（A点处）10米的建筑物是否需要拆除？（参考数据： ≈1.414， ≈1.732）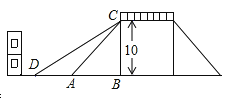

参考答案：

【答案】解：需要拆除，理由为：
∵CB⊥AB ， ∠CAB=45°，
∴△ABC为等腰直角三角形，
∴AB=BC=10米，
在Rt△BCD中，新坡面DC的坡度为i= ：3，即∠CDB=30°，
∴DC=2BC=20米，BD= 米，
∴AD=BD-AB=（10 -10）米≈7.32米，
∵3+7.32=10.32＞10，
∴需要拆除 ．
【解析】需要拆除，理由为：根据题意得到三角形ABC为等腰直角三角形，求出AB的长，在直角三角形BCD中，根据新坡面的坡度求出∠BDC的度数为30，利用30度所对的直角边等于斜边的一半求出DC的长，再利用勾股定理求出DB的长，由DB-AB求出AD的长，由AD+3与10比较即可得到结果 ．

关闭