【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值) . 
参考答案:
【答案】解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F , 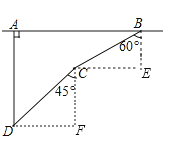
则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF .
在Rt△BCE中,∵∠E=90°,∠CBE=60°,
∴∠BCE=30°,
∴BE= ![]() BC=
BC= ![]() ×1000=500米;
×1000=500米;
在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=AB=1000米,
∴CF= ![]() CD=500
CD=500 ![]() 米,
米,
∴DA=BE+CF=(500+500 ![]() )米,
)米,
故拦截点D处到公路的距离是(500+500 ![]() )米 .
)米 .
【解析】过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F , 则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF . 解Rt△BCE , 求出BE= ![]() BC=
BC= ![]() ×1000=500米;解Rt△CDF , 求出CF=
×1000=500米;解Rt△CDF , 求出CF= ![]() CD=500
CD=500 ![]() 米,则DA=BE+CF=(500+500
米,则DA=BE+CF=(500+500 ![]() )米 .
)米 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.
(1)求证:△CBE为等边三角形;
(2)若AD=5,DE=7,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=
 :3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:  ≈1.414,
≈1.414,  ≈1.732)
≈1.732)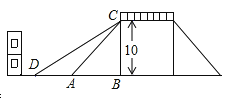
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到1′) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列条件的△ABC , 不是直角三角形的是( )
A.∠C=∠A+∠B
B.a:b:c=3:4:5
C.∠C=∠A-∠B
D.∠A:∠B:∠C=3:4:5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

相关试题

