【题目】如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D , E , F , G , 已知∠CGD=42°
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B , 交AC边于点H , 如图②所示,点H , B在直尺上的度数分别为4,13.4,求BC的长(结果保留两位小数).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
参考答案:
【答案】
(1)
解:∵∠CGD=42°,∠C=90°,
∴∠CDG=90°-42°=48°,
∵DG∥EF,
∴∠CEF=∠CDG=48°;
(2)
解:∵点H,B的读数分别为4,13.4,
∴HB=13.4-4=9.4(m),
∴BC=HBcos42°≈9.4×0.74≈6.96(m).
答:BC的长为6.96m.
【解析】(1)先根据直角三角形的两锐角互为求出∠CDG的度数,再根据两直线平行,同位角相等求出∠DEF , 然后根据三角形的一个外角等于与它不相邻的两个内角的和即可求出∠EFA;(2)根据度数求出HB的长度,再根据∠CBH=∠CGD=42°,利用42°的余弦值进求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=4km , 某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为km .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC.BD相交于点O , 过点O作OE⊥AC交AD于E , 若AB=6,AD=8,求sin∠OEA的值 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形共有_____对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.
(1)求证:△CBE为等边三角形;
(2)若AD=5,DE=7,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=
 :3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:  ≈1.414,
≈1.414,  ≈1.732)
≈1.732)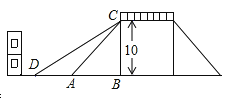
相关试题

