【题目】如图, ![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 延长线上任意一点,以
延长线上任意一点,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,且
,且![]() ,连结
,连结![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )在点
)在点![]() 运动过程中,试问
运动过程中,试问![]() 的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
(![]() )已知
)已知![]() ,设
,设![]() ,
, ![]() .
.
①试求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
②当![]() 时,求
时,求![]() 的外接圆半径.
的外接圆半径.

参考答案:
【答案】(![]() )见解析;(
)见解析;(![]() )结论:
)结论: ![]() 的度数是定值,
的度数是定值, ![]() ;(
;(![]() )①
)①![]() ,
,
②![]() 的外接圆的半径为
的外接圆的半径为![]() .
.
【解析】试题分析: ![]() 设
设![]() 与
与![]() 交于点
交于点![]() ,由
,由![]() ,推出
,推出![]() ,,推出
,,推出![]() ,
, ![]() ,推出
,推出![]() ,
,
推出![]() ,由
,由![]() ,推出
,推出![]() ,即可解决问题.
,即可解决问题.
(2)结论: ![]() 的度数是定值,
的度数是定值, ![]() .由(1)可知△
.由(1)可知△![]() ,即可推出
,即可推出![]()
(3)①在![]() 中,由
中,由![]() ,推出BC=AC=1,在
,推出BC=AC=1,在![]() 中,
中, ![]() ,由
,由![]() ,推出
,推出![]() ,推出
,推出![]() ,可得
,可得![]() ,根据
,根据![]() 计算即可.②取
计算即可.②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
,
由![]() 推出
推出![]() 推出点
推出点![]() 是
是![]() 的外接圆的圆心,求出线段
的外接圆的圆心,求出线段![]() 即可解决问题.
即可解决问题.
试题解析:(![]() )证明:如图,设
)证明:如图,设![]() 与
与![]() 交于点
交于点![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )结论:
)结论: ![]() 的度数是定值,
的度数是定值, ![]() .
.
理由:由(![]() )可知
)可知![]() ,
,
∴![]() ,
,
∴点![]() 运动过程中,
运动过程中, ![]() 的度数是定值,
的度数是定值,
![]() .
.
(![]() )①在
)①在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
![]() .
.
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点![]() 是
是![]() 的外接圆的圆心,
的外接圆的圆心,
∵![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
∴![]() ,
,
由(![]() )可知
)可知![]() ,
,
∴![]() ,
,
在![]() 中,
中,
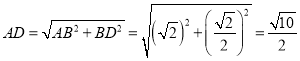 ,
,
∴![]() .
.
∴![]() 的外接圆的半径为
的外接圆的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
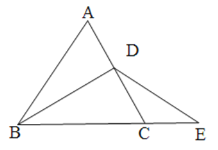
图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.
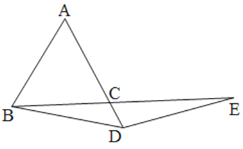
图2
-
科目: 来源: 题型:
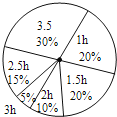
查看答案和解析>>【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h)
1
1.5
2
2.5
3
3.5
人数
72
36
54
18
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第100个图中正方形和等边三角形的个数之和是( )

A. 900 B. 903 C. 906 D. 807
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
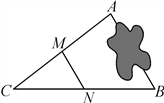
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
相关试题

