【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
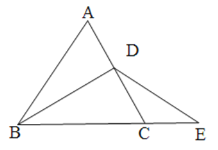
图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.
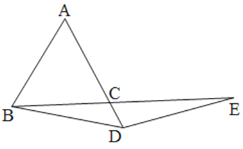
图2
参考答案:
【答案】(1)详见解析;(2)详见解析
【解析】
(1)求出∠E=∠CDE,推出CD=CE,根据等腰三角形性质求出AD=DC,即可得出答案;解:(1)AD=CE,理由:过D作DF∥AB交BC于E,
(2)(1)中的结论仍成立,如图3,过点D作DP∥BC,交AB的延长线于点P,证明△BPD≌△DCE,得到PD=CE,即可得到AD=CE.
解:(1)AD=CE,
证明:如图1,过点D作DP∥BC,交AB于点P,
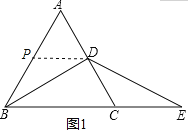
∵△ABC是等边三角形,
∴△APD也是等边三角形,
∴AP=PD=AD,∠APD=∠ABC=∠ACB=∠PDC=60°,
∵DB=DE,
∴∠DBC=∠DEC,
∵DP∥BC,
∴∠PDB=∠CBD,
∴∠PDB=∠DEC,
又∠BPD=∠A+∠ADP=120°,∠DCE=∠A+∠ABC=120°,
即∠BPD=∠DCE,
在△BPD和△DCE中,∠PDB=∠DEC,∠BPD=∠DCE,DB=DE,
∴△BPD≌△DCE,
∴PD=CE,
∴AD=CE;
(2)如图3,过点D作DP∥BC,交AB的延长线于点P,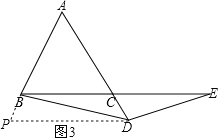
∵△ABC是等边三角形,
∴△APD也是等边三角形,
∴AP=PD=AD,∠APD=∠ABC=∠ACB=∠PDC=60°,
∵DB=DE,
∴∠DBC=∠DEC,
∵DP∥BC,
∴∠PDB=∠CBD,
∴∠PDB=∠DEC,
在△BPD和△DCE中,
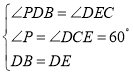
∴△BPD≌△DCE,
∴PD=CE,
∴AD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 边
边 ,
, ,沿
,沿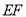 折叠,使
折叠,使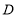 点与
点与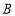 点重合,
点重合,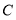 点的对应点为
点的对应点为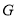 ,将
,将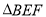 绕着点
绕着点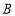 顺时针旋转,旋转角为
顺时针旋转,旋转角为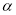
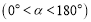 .记旋转过程中的三角形为
.记旋转过程中的三角形为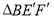 ,在旋转过程中设直线
,在旋转过程中设直线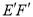 与射线
与射线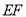 、射线
、射线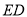 分别交于点
分别交于点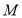 、
、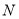 ,当
,当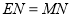 时,则
时,则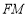 的长为_______.
的长为_______.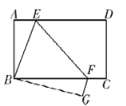
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(
 )
) 分别取
分别取 ,
, 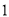 ,
,  时,试求出各函数表达式,并说出这三个函数的一个共同点.
时,试求出各函数表达式,并说出这三个函数的一个共同点.(
 )对于任意负实数
)对于任意负实数 ,当
,当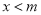 时,
时,  随
随 的增大而增大,试求出
的增大而增大,试求出 的最大整数值.
的最大整数值.(
 )点
)点 ,
,  是函数图象上两个点,满足若
是函数图象上两个点,满足若 ,试比较
,试比较 和
和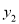 的大小关系.
的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>1时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
-
科目: 来源: 题型:
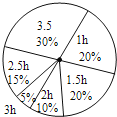
查看答案和解析>>【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h)
1
1.5
2
2.5
3
3.5
人数
72
36
54
18
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第100个图中正方形和等边三角形的个数之和是( )

A. 900 B. 903 C. 906 D. 807
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中,  ,
,  ,点
,点 是线段
是线段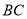 延长线上任意一点,以
延长线上任意一点,以 为直角边作等腰直角
为直角边作等腰直角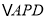 ,且
,且 ,连结
,连结 .
.(
 )求证:
)求证:  .
.(
 )在点
)在点 运动过程中,试问
运动过程中,试问 的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.(
 )已知
)已知 ,设
,设 ,
,  .
.①试求
 关于
关于 的函数表达式.
的函数表达式.②当
 时,求
时,求 的外接圆半径.
的外接圆半径.
相关试题

