【题目】如图,在矩形ABCD中,AB=15,BC=8,E是AB上一点,沿DE折叠使A落在DB上,求AE的长. 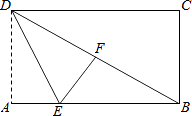
参考答案:
【答案】解:∵四边形ABCD是矩形,∴AD=BC=8, 由折叠性质可知:DF=AD=BC=8,EF=EA,EF⊥BD.
在Rt△BAD中,由勾股定理得:BD= ![]() =
= ![]() =17,
=17,
∵BF=BD﹣DF,
∴BF=17﹣8=9.
设AE=EF=x,则BE=15﹣x.
在Rt△BEF中,由勾股定理可知:EF2+BF2=BE2 ,
即x2+92=(15﹣x)2 ,
解得:x= ![]() .
.
∴AE= ![]() .
.
【解析】由勾股定理可求得BD=17,由翻折的性质可求得BF=9,EF=EA,EF⊥BD,设AE=EF=x,则BE=15﹣x,在Rt△BEF中,由勾股定理列方程求解即可.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x方程3x+5m﹣6=0的解是x=﹣3,那么m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=
 x-3与反比例函数y=
x-3与反比例函数y= 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=
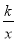 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(1,2)是反比例函数
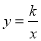 图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是 .
图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是 .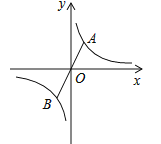
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)7(3﹣x)﹣5(x﹣3)=8
(2) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F在OD上一点,且∠1=∠A.
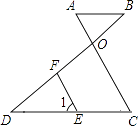
(1)求证:FE∥OC;
(2)若∠DFE=70°,求∠BOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个外角都等于60°,则这个多边形的边数为( )
A.8
B.7
C.6
D.5
相关试题

