【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题: 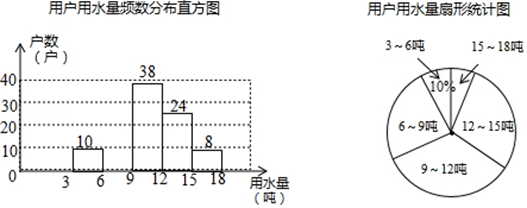
(1)此次抽样调查的样本容量是;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?
参考答案:
【答案】
(1)100
(2)解:6~9吨的户数为100﹣(10+38+24+8)=20(户),
补全频数分布直方图如下:
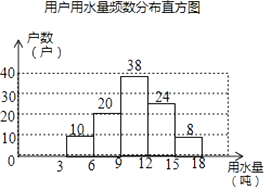
扇形图中“6吨﹣﹣9吨”部分的圆心角的度数为360°× ![]() =72°;
=72°;
(3)解:1000× ![]() =680,
=680,
答:该社区约有680户家庭的用水全部享受基本价格.
【解析】解:(1)此次抽样调查的样本容量是10÷10%=100, 所以答案是:100;
【考点精析】关于本题考查的总体、个体、样本、样本容量和频数分布直方图,需要了解所要考察的全体对象叫总体,组成总体的每一个考察对象叫个体,被抽取的那部分个体组成总体的一个样本,样本中个体的数目叫这个样本的容量(样本容量没有单位);特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)才能得出正确答案.
-
科目: 来源: 题型:
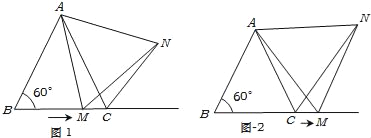
查看答案和解析>>【题目】如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.
(1)当∠BAM= °时,AB=2BM;
(2)请添加一个条件: ,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:BM=CN;
②如图2,当点M运动到线段BC之外时,其它条件不变,①中结论BM=CN还成立吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC边
 上的高,BE平分∠△ABC交AD于点E.若∠C=60°,∠BED=70°. 求∠ABC和∠BAC的度数.
上的高,BE平分∠△ABC交AD于点E.若∠C=60°,∠BED=70°. 求∠ABC和∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.
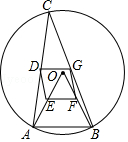
(1)试判断四边形DEFG的形状,并说明理由;
(2)填空: ①若AB=3,当CA=CB时,四边形DEFG的面积是;
②若AB=2,当∠CAB的度数为时,四边形DEFG是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
我们知道
 的几何意义是在数轴上数
的几何意义是在数轴上数 对应的点与原点的距离,即
对应的点与原点的距离,即 =
=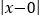 ,也就是说,
,也就是说, 表示在数轴上数
表示在数轴上数 与数0对应的点之间的距离;这个结论可以推广为
与数0对应的点之间的距离;这个结论可以推广为 表示在数轴上数
表示在数轴上数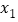 与数
与数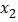 对应的点之间的距离;
对应的点之间的距离;例1.解方程|
 |=2.因为在数轴上到原点的距离为2的点对应的数为
|=2.因为在数轴上到原点的距离为2的点对应的数为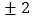 ,所以方程|
,所以方程| |=2的解为
|=2的解为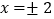 .
.例2.解不等式|
 -1|>2.在数轴上找出|
-1|>2.在数轴上找出| -1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|
-1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程| -1|=2的解为
-1|=2的解为 =-1或
=-1或 =3,因此不等式|
=3,因此不等式| -1|>2的解集为
-1|>2的解集为 <-1或
<-1或 >3.
>3.
例3.解方程|
 -1|+|
-1|+| +2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的
+2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的 的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的
的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的 对应的点在1的右边或-2的左边.若
对应的点在1的右边或-2的左边.若 对应的点在1的右边,可得
对应的点在1的右边,可得 =2;若
=2;若 对应的点在-2的左边,可得
对应的点在-2的左边,可得 =-3,因此方程|
=-3,因此方程| -1|+|
-1|+| +2|=5的解是
+2|=5的解是 =2或
=2或 =-3.
=-3.
参考阅读材料,解答下列问题:
(1)方程|
 +3|=4的解为 ;
+3|=4的解为 ;(2)解不等式:|
 -3|≥5;
-3|≥5;(3)解不等式:|
 -3|+|
-3|+| +4|≥9
+4|≥9
相关试题

